해당 포스팅은 "실전 시계열 분석" 교재와 실습코드 / 고려대학교 DMQA 강의와 강의자료를 기반으로 작성되었습니다.

https://www.youtube.com/watch?v=ma_L2YRWMHI&list=PLpIPLT0Pf7IqSuMx237SHRdLd5ZA4AQwd&index=9
1. 시계열 데이터와 선형 회귀 ?
시계열 데이터에는 통상적으로 회귀 모델을 사용하지 않는다.
그 이유는 선형 회귀 분석의 가정인 독립 항등분포 (Independently and Identically Distributed) 조건이 시계열 데이터에서는 성립하지 않는 경우가 대부분이기 때문이다.
시계열 데이터는 그 시간 step에 영향이 클수록 시간과 강한 상관관계를 가지고 있기에 위 가정이 성립되지 않아 선형 회귀를 쓰는 것이 바람직하지 않다는 것이다.
반대로, 이 책에서도 시간과의 강한 상관관계가 없다면 선형회귀 모델링을 시도하는 것은 유의미할 수도 있다고 말한다.
2. Exponential Smoothing (지수 평활법)
2-1. Basic
지수평활법은 다음과 같은 특징을 가진다.
- 이전 데이터의 가중 평균을 통해 다음 step의 값을 예측한다.
- 가중 평균을 하는데 있어 지수 분포에 근거한 가중치를 부여한다.
- 최근 데이터에 더 많은 가중치를 부여하며 과거 데이터에 부여하는 가중치는 과거일수록 줄어든다.
- 모든 과거 데이터를 포함해 계산한다.
가중치 $\alpha$ 는 0과 1 사이의 값으로 각 시점에 대해 아래와 같은 가중치가 부여된다.
- 시점 t 가중치 = $\alpha$
- 시점 t -1 가중치 = $\alpha(1- \alpha)$
- 시점 t-2 가중치 = $\alpha(1- \alpha)^{2}$
이러한 이유로 과거 데이터에는 더 적은 가중치가 부여되고 가중치들이 지수 분포를 띄게 되어 지수평활법이라 명명되었다.
구체적인 계산 방식은 아래와 같다.

- $L_{0}$ 계산 : $L_{0}$ = $\frac{1}{n}\sum_{i=1}^{n}Di$
- $L_{t+1}$ 계산 : $L_{t+1} = \alpha D_{t+1} + (1-\alpha) L_{t}$
- 예측
- $F_{t+1}$ = $L_{t}$
- $F_{t+n}$ = $L_{t}$
- $F_{t+1}$ = $L_{t}$
위 방식대로 $\alpha$ = 0.1 로 계산한 결과가 위 이미지의 표의 실제 수치와 일치하는 것을 확인할 수 있다.
이 때 $\alpha$가 크다면 최근 데이터에 큰 가중치를 부여하는 것이고 $\alpha$가 작다면 과거 데이터에 큰 가중치를 부여하게 된다.
통상적으로 $\alpha$는 0.2 또는 0.3 값을 가지나 정답데이터가 존재한다면 최적의 $\alpha$는 그 오차를 최소화할 수 있는 값으로 설정되고 이는 패키지를 통해 자동적으로 고정할 수 있다.
하지만 지수평활법은 다음과 같은 한계점을 가진다.
- 트렌드가 있는 데이터에 사용하는 것은 부적합하다.
- 계절적 변동이 있는 데이터에 사용하는 것은 부적합하다.
- 미래 시점에 관계없이 예측값이 모두 동일하다.
2-2. Double Exponential Smoothing (이중지수 평활법)
기본적인 메커니즘은 단순 지수 평활법과 동일한데 이중지수 평활법은 트렌드가 있는 데이터에 적합한 방법이다.
계산 방식은 다음과 같다.

- level인 $L_{0}$, trend인 $B_{0}$ 를 결정
- time step을 x변수, value를 y변수로 하는 회귀분석식 y = $\beta0$ + $\beta1$x 를 산출
- $\beta0$ = $L_{0}$
- $\beta1$ = $B_{0}$
- time step을 x변수, value를 y변수로 하는 회귀분석식 y = $\beta0$ + $\beta1$x 를 산출
- $L_{t+1}$ 계산 : $L_{t+1} = \alpha D_{t+1} + (1-\alpha) (L_{t} + B_{t})$
- $B_{t+1}$ 계산 : $\beta(L_{t+1} - L_{t}) + (1-\beta)B_{t}$
- 예측
- $F_{t+1}$ = $L_{t}$ + $B_{t}$
- $F_{t+2}$ = $L_{t}$ + 2 $B_{t}$
- $F_{t+n}$ = $L_{t}$ + n $B_{t}$
- $F_{t+1}$ = $L_{t}$ + $B_{t}$
3. Holt - Winter
홀트 윈터스 모형은 이중지수평활법은 발전된 버전으로 이전까지의 모델이 계절적 변동은 다루지 못한 것에 비해 홀트 윈터스 모형은 계절적 변동을 반영해 평활한다.
가법(additive)과 승법(multiplicative)모형이 존재하며 가법 모형은 계절 변동 산포가 일정할때, 승법 모형은 산포가 증가할 때 사용한다.
각각의 계산 방식은 다음과 같다.
3-1. Additive
- Level : $l_{T}$ = $\alpha (y_{T} - sn_{T-L}) + (1-\alpha) (l_{T-1} + b_{T-1})$
- Trend : $b_{T}$ = $\gamma (l_{T} - l_{T-1}) + (1-\gamma) b_{T-1}$
- Seasonal : $sn_{T}$ = $\delta (y_{T} - l_{T})$ - $(1-\delta) sn_{T-1}$
- Prediction : $y_{T+\tau}(T)$ = $l_{T} + \tau b_{T} + sn_{T+\tau-L}$
3-2. Multiplicative
- Level : $l_{T}$ = $\alpha (y_{T} / sn_{T-L}) + (1-\alpha) (l_{T-1} + b_{T-1})$
- Trend : $b_{T}$ = $\gamma (l_{T} / l_{T-1}) + (1-\gamma) b_{T-1}$
- Seasonal : $sn_{T}$ = $\delta (y_{T} / l_{T})$ - $(1-\delta) sn_{T-1}$
- Prediction ($예측시점 = \tau$) : $y_{T+\tau}(T)$ = $l_{T} + \tau b_{T} sn_{T+\tau-L}$
4. Autoregressive, AR (자기회귀모델)
AR, 자기회귀 모델은 과거가 미래를 예측한다는 직관적 사실을 기반으로 특정 시점 t의 값은 이전 시점들을 구성하는 값들의 함수라는 시계열 가정을 가진다.
즉, 다시 말해 AR model = Model that use lags of the dependent variable as independent variables.
식으로 표현하면 다음과 같다.
$y_{t}$ = $\phi_{0}$ + $\phi_{1} y_{t-1}$ + $\phi_{2} y_{t-2}$ + $\cdots$ +$\phi_{p} y_{t-p}$ + $\varepsilon_{t}$
식을 보면 다항변수와 각각의 $\phi$ 기울기, 그리고 절편 $\phi_{0}$, errot term $\varepsilon$ 으로 이루어진 회귀식과 형태가 유사하다.
하지만 이전에서도 언급했듯이 independence 가정이 성립되지 않는다.
예측하는 $y_{t}$ 를 그 이전 시점의 $y$들로 예측하기 때문이다.
이 때, 과거 시점을 얼마나 사용할지, 즉 p를 어떻게 설정하지는 모델을 구성하는 사람에게 달려 있다.
5. Moving Average, MA (이동평균법)
MA 이동평균법은 각 시점의 데이터가 최근 과거 값에 대한 오차항으로 구성된 함수로 표현된다.
즉, 다시 말해 MA = Model that use past errors that follow a white noise distribution as explanatory variables
이 때 오차항은 white noise 분포를 따른다고 하였는데 이는 평균이 0인 독립항등분포를 의미한다.
식으로 표현하면 다음과 같다.
$y_{t}$ =$\theta_{0}$ + $\varepsilon_{t}$ + $\theta_{1} \cdot \varepsilon_{t-1}$ + $\theta_{2} \cdot \varepsilon_{t-2}$ + $\cdots$ + $\theta_{q} \cdot \varepsilon_{t-q}$
MA 모델도 마찬가지로 q는 사용자가 결정한다.
6. Autoregressive Moving Average, ARMA
ARMA 모델은 명칭대로 AR과 MA 모델을 합친 것이다.
수식 또한 위에서 정의한 AR, MA의 두 $y_{t}$ 전개식을 그대로 더한 것과 같다.
7. Stationary (정상성) 와 Nonstationary(비정상성)
AR, MA, ARMA 모델을 다뤄봤는데 한가지 주의할 점은 이 세가지 모델은 모두 시계열 데이터가 정상성을 띌 때 사용할 수 있다는 것이다.
정상성이란 평균, 분산, 공분산 등의 통계적 속성이 시간에 대해 일정한 시계열을 의미한다.
정상성은 미래에 대한 모델링과 예측을 정확하게 해주기에 시계열에서의 바람직한 특성이다.
반대로 비정상성은 정상성으로의 변환이 필요하다.
비정상성의 예제는 다음과 같다.
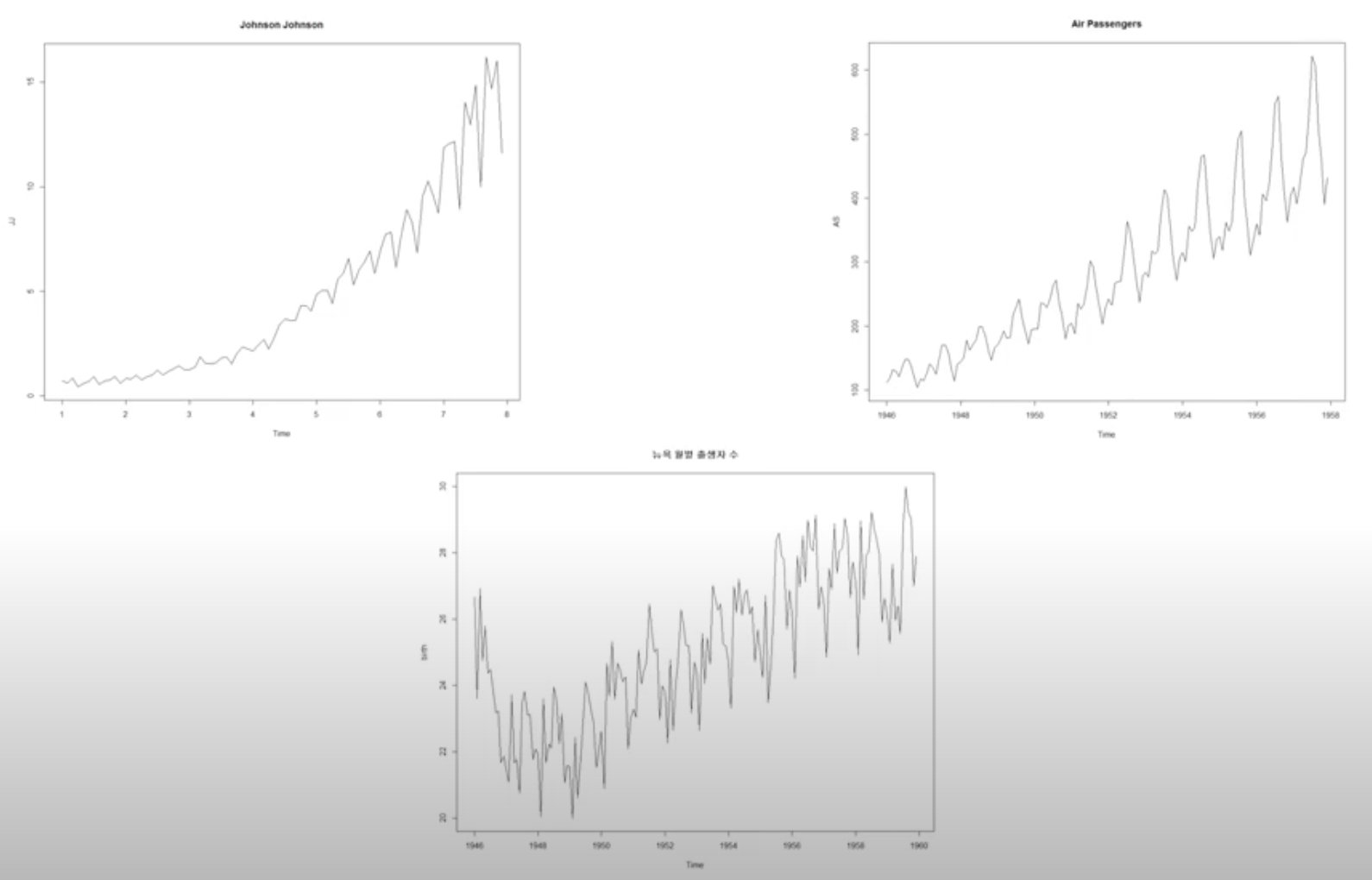
따라서 시계열 데이터가 주어졌고, AR, MA, ARMA 모델을 사용하길 바란다면 정상성에 대한 검정이 이뤄져야 한다.
정상성에 대한 검정은 여러가지가 있지만 그 중 ACF 검정에 대해 알아보자.
다른 검정 방식은 다음 포스팅에서 다루었다.
2023.02.02 - [Advance Deep Learning/[Quant] 금융 파이썬 쿡북] - 시계열 정상성 검정 & 교정
시계열 정상성 검정 & 교정
"금융 파이썬 쿡북 Ch3. 시계열 모델링 "의 내용을 기반으로 작성하였습니다. (실습 깃헙) 1. 정상성 정상성(stationary) 시계열이란 평균, 분산, 공분산 등의 통계적 속성이 시간에 대해 일정한 시계
needmorecaffeine.tistory.com
7-1. ACF (Auto Correlation Function, 자기상관함수) 와 PACF (Partial Auto Correlation Function, 부분자기상관함수)
ACF는 시간에 따른 상관정도를 나타낸 것으로 현재 상태가 과거와 미래의 데이터와 밀접한 관련이 있는 것을 자기상관관계가 크다라고 표현한다.
자기상관관계가 큰 데이터로는 주가가 있을 수 있는데 오늘의 주가가 어제의 주가에 큰 영향을 받는다는 직관적인 판단으로도 알 수 있다.
먼저 Auto Covariance를 살펴보면 다음과 같다.
시점 t와 h 시점 이후의 시점 간의 자기상관계수는 다음과 같이 정의된다.
$\gamma_{x}(h)$ = $Cov(X_{t}, X_{t+h})$
한가지 성질, $\gamma_{x}(0)$ = V(X_{t} 라는 것을 짚자.
이렇게 정의된 Auto Covariance로 Auto Correlation은 다음과 정의된다.
$\rho_{x}(h)$ = $\frac{Cov(X_{t}, X_{t+h})}{\sqrt (V(X_{t})V(X_{t+h}))}$ = $\frac{\gamma_{x}(h)}{\gamma_{x}(0)}$
그리고 PACF, 부분자기상관함수에 대해 알아보면 다음과 같다.
부분자기상관계수는 $X_{t}$와 k 시점 이후 $X_{t+K}$ 에서 그 사이 시점인 $X_{t+1}$ 부터 $X_{t+k-1}$의 효과를 제거한 상관계수를 의미한다.
각각 시점의 효과를 제거한 결과를 다음과 같이 표기하고
$X_{t}^*$ = $X_{t}$ - $E(X_{t} | X_{t+1}, \cdots , X_{t+k-1})$
$X_{t+k}^*$ = $X_{t+k}$ - $E(X_{t+k} | X_{t+1}, \cdots , X_{t+k-1})$
부분자기상관계수는 다음과 같이 정의된다.
$\phi_{kk}$ = Corr($X_{t}^*$, $X_{t+k}^*$)
더 자세한 얘기는 다루지 않겠지만 PACF는 위와 같이 중간 시점의 효과를 제거함으로써 시간의 효과, 즉 trend를 제거한 후 시계열 데이터를 살펴보기 위한 적절한 방법이라 할 수 있다.
7-2. ACF, PACF를 통한 정상성 확인
위에서 이론적으로 다룬 ACF와 PACF를 기반으로 정상성을 확인하는 방법은 다음과 같다.
주어진 시계열 데이터를 ACF, PACF plot을 그리고 그 패턴을 확인한다.
다음은 예시이다.
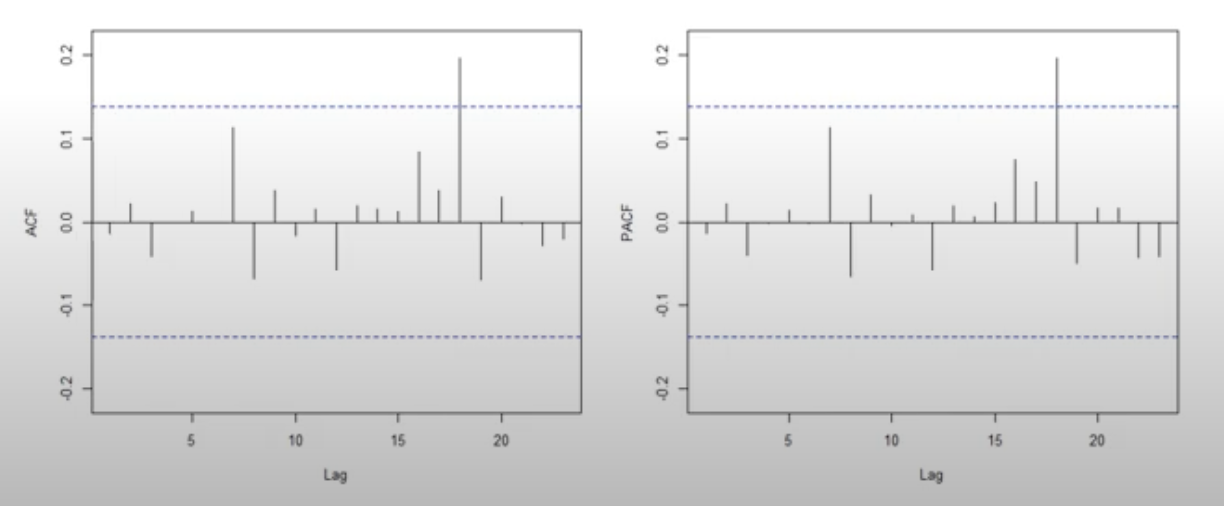
plot을 보면 x축에 lag가 있는데 lag = k일 경우 이는 현재 데이터와 k 시점 이전의 데이터와의 autocorrelation과 partial autocorrelation을 의미한다.
다음은 비정상 데이터와 그 ACF, PACF plot이다.
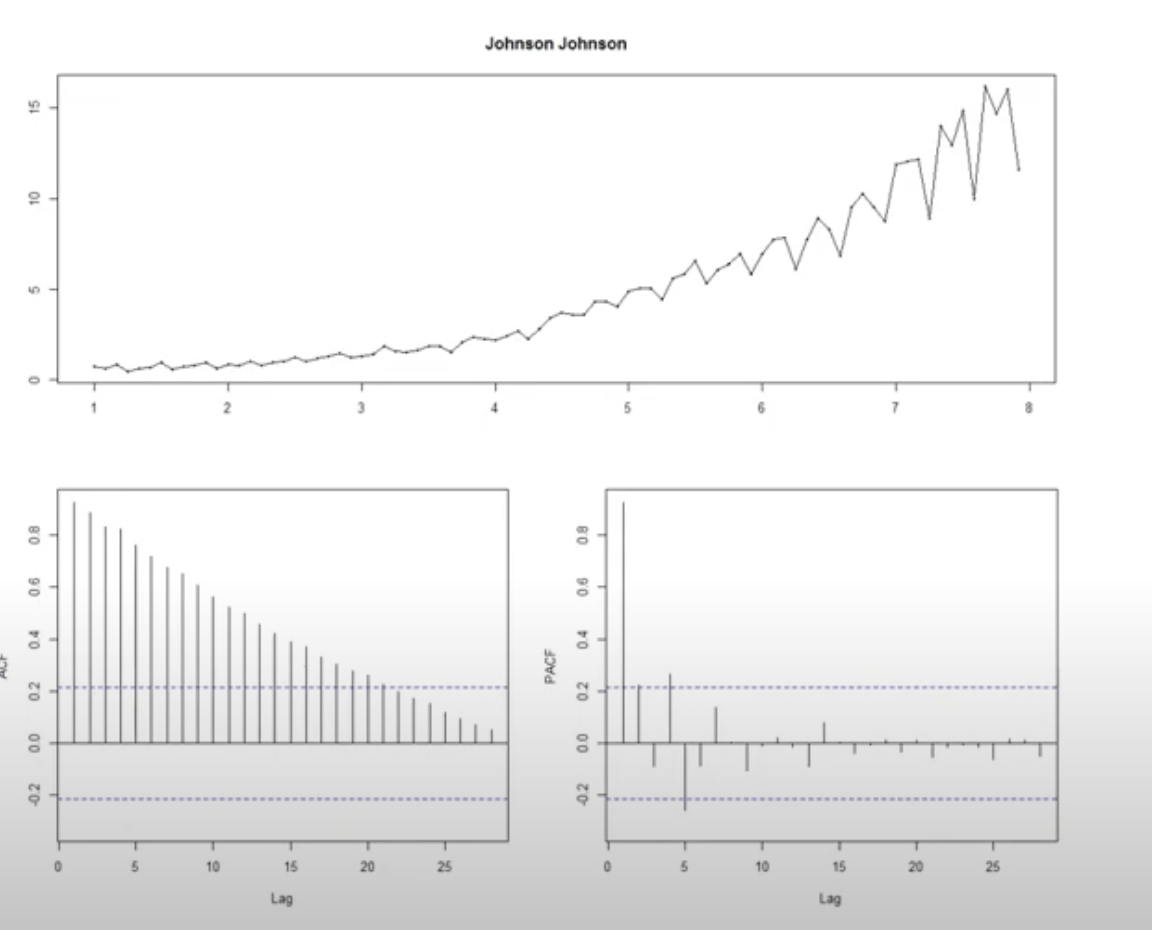

ACF plot을 보면 상관계수가 천천히 감소하고 있음을 확인할 수 있다.
PACF plot의 경우 그 파란색 점선 (정상성 검정을 위한 유의수준)을 넘어서는 lag 지점이 존재한다.
이런 특성을 가진 경우 비정상성을 띈다고 판단한다.
7-3. 비정상성에서 정상성으로, 차분
그렇다면 비정상성 데이터를 정상성으로 바꾸고 AR, MA, ARMA 모델을 적용할 방법은 없을까?
대표적으로 수행되는 방법이 Differencing, 차분이다.
1차, 2차 차분은 다음과 같이 정의된다.
($Y_{t}^n$은 n차 차분된 결과를 의미, n 제곱 아님)
- 1차 차분 : $Y_{t}^1$ = $X_{t}$ - $X_{t-1}$
- 2차 차분 : $Y_{t}^2$ = ($X_{t}$ - $X_{t-1}$) - ($X_{t-1}$ - $X_{t-2}$) = $X_{t}$ - 2$X_{t-1}$ + $X_{t-2}$
즉, n 시점 이전의 데이터와 현재 데이터의 차이를 구하고 이렇게 구한 데이터로 다시 시계열 데이터를 구성하는 것이다.
당연 정상성을 띄고 있을 때 이 차분 작업을 필요가 없지만 비정상성 데이터가 일정한 트렌드를 가지고 있을 경우, 1차 차분이 적용되면 대다수의 경우 정상성을 띄게 되고,
그렇지 않은 데이터라도 통상적으로 최대 2차 차분까지만 진행해 정상성을 다시 확인한다.
다음 장에서는 다룬 내용을 기반으로 실습을 해보겠다.
Ref
- Oreilly "실전시계열 분석" 6장
- https://zephyrus1111.tistory.com/169
- https://www.youtube.com/watch?v=ma_L2YRWMHI&list=PLpIPLT0Pf7IqSuMx237SHRdLd5ZA4AQwd&index=9
[시계열 분석] 9. (Augmented) Dickey-Fuller Test(검정) with Python
이번 포스팅에서는 단위근 검정을 위한 대표적인 방법으로 Dickey-Fuller Test(검정)과 이를 확장한 Augmented Dickey Fuller Test(검정)에 대한 내용을 알아본다. 또한 Python(파이썬)을 이용하여 (Augmented) Dickey
zephyrus1111.tistory.com
'Time Series Analysis' 카테고리의 다른 글
| Facebook Prophet 논문 리뷰 (0) | 2023.05.15 |
|---|---|
| 시계열 통계모델 2 [이론] - ARCH / GARCH 모형 (0) | 2023.03.30 |
| 시계열 통계모델 2 [이론] - ARIMA / SARIMA / VAR 모형 (0) | 2023.03.20 |
| 시계열 데이터 EDA (0) | 2023.03.09 |
| 누락된 시계열 데이터 (1) | 2023.03.07 |