해당 포스팅은 "실전 시계열 분석" 교재와 실습코드를 기반으로 작성되었습니다.

1. Plot 그리기
R이 제공하는 Eustockmarkets 시계열 데이터셋으로 시각화 해보자.
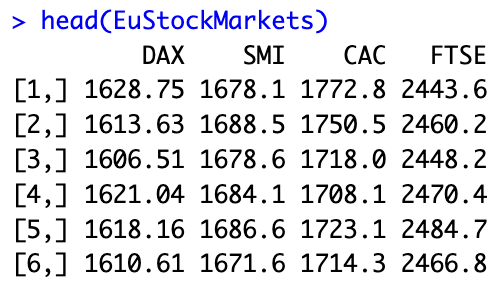
plot(EuStockMarkets)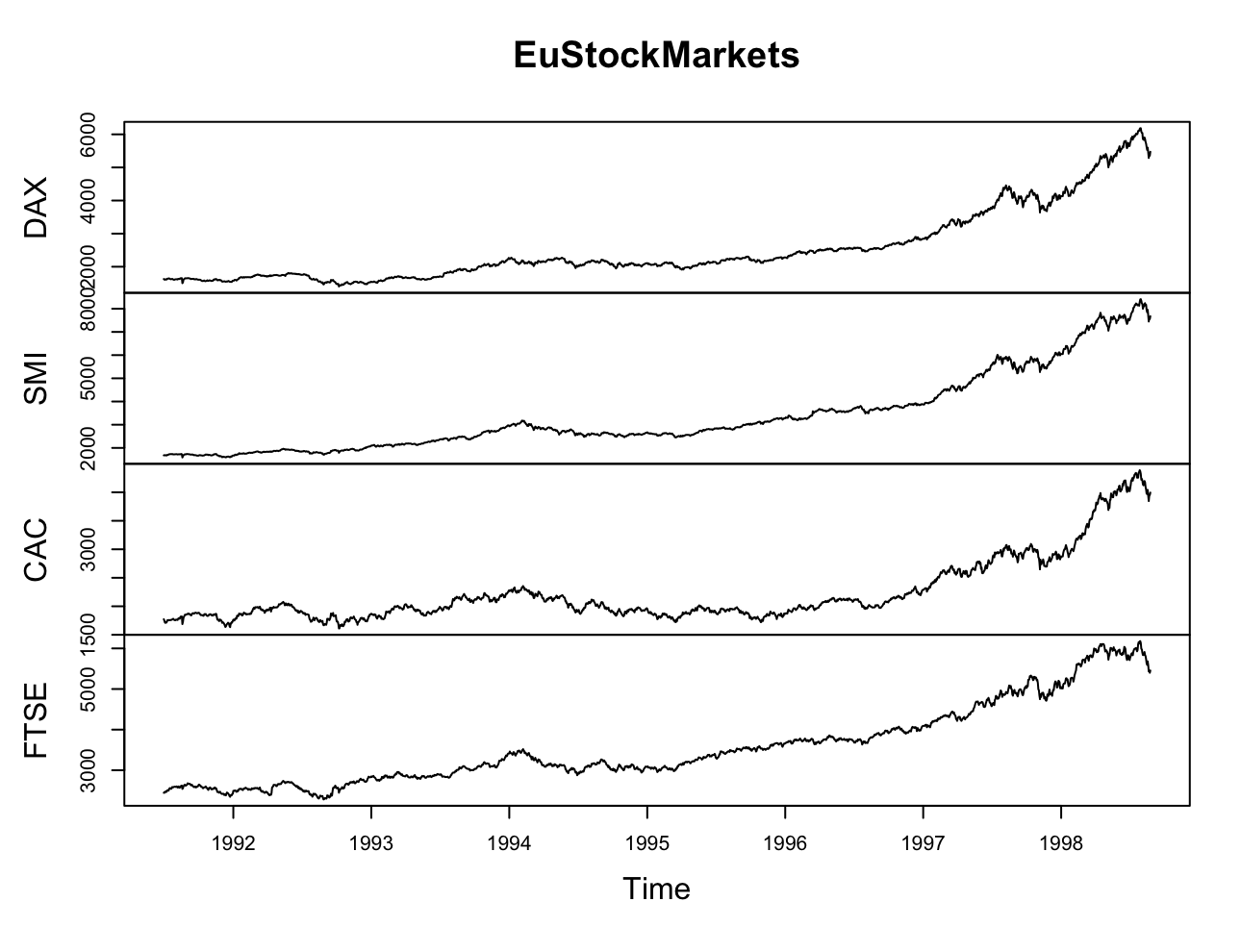
간단하게 plot() 함수만으로도 데이터를 서로 다른 시계열 그래프로 자동 분할할 수 있다.
class(EuStockMarkets)
이 명령어로 R의 ts와 mts 객체를 사용한다는 것을 알 수 있다. ts 객체는 R의 여러 패키지들이 활용하고 있으며 위 plot()함수와 같이 적절한 도표를 바로 반환해줄 수 있다.
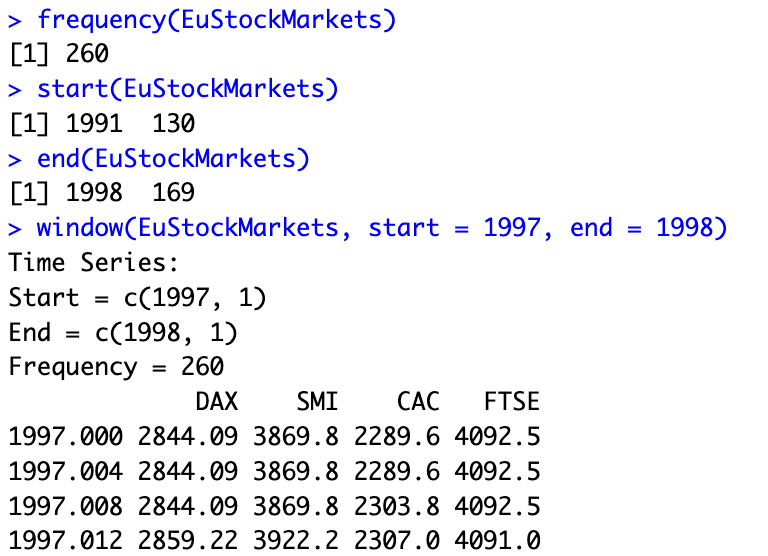
다른 기본 기능들은 다음과 같다.
1-1. 히스토그램
히스토그램도 간단하게 만들 수 있다.
단 이때 시간상 인접한 데이터 간의 차이(차분)된 결과도 함께 보겠다.
> hist(EuStockMarkets[, "SMI"], 30)
> hist(diff(EuStockMarkets[,"SMI"],30))

변형을 가하지 않은 원래 데이터는 매우 넓게 퍼져있음을 알 수 있다. 이는 내재된 추세를 반영한 결과이기 때문이다.
하지만 차분한 데이터의 경우 데이터가 모여있고 일정 부분 정규분포의 형태를 따른다고 할 수 있다.
이렇게 차분된 결과는 실제 측정치가 아닌 한 측정치가 다음 측정치로 변환한 정도를 나타내는 것으로 시계열 데이터를 탐색하는 목적에 부합한 변형이라고 할 수 있다.
특히 금융 도메인의 경우, 그 추세가 그대로 내재된 데이터를 사용하는 것은 정확한 정보를 제공하지 못한다는 것을 유의해야 한다.
1-2. 산점도
산점도를 통해 특정 시간에 대한 두 주식의 관계와 두 주식의 시간에 따른 각각의 가격 변동이 갖는 연관성을 확인할 수 있다.
> plot(EuStockMarkets[,"SMI"], EuStockMarkets[,"DAX"])
> plot(diff(EuStockMarkets[,"SMI"]), diff(EuStockMarkets[,"DAX"]))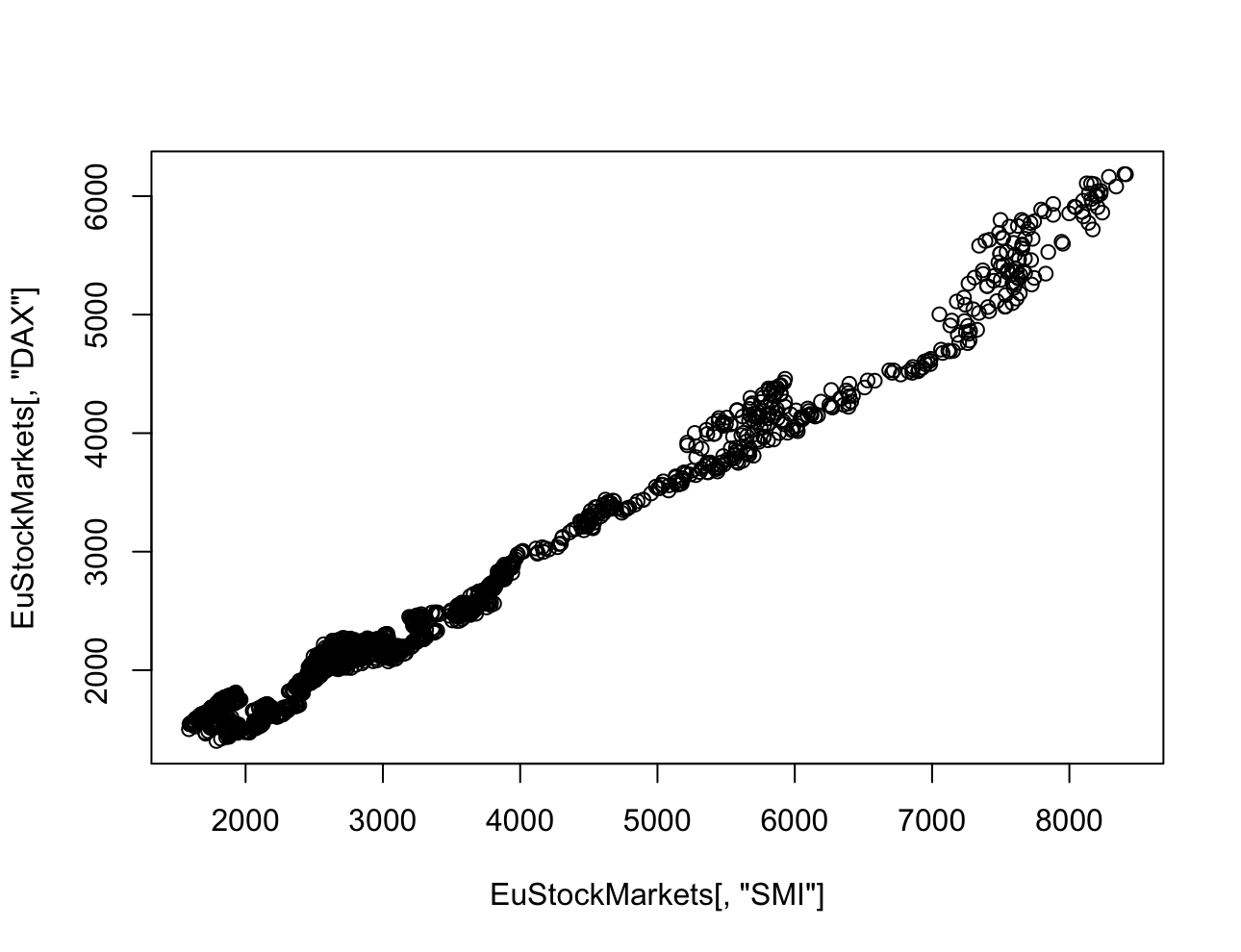
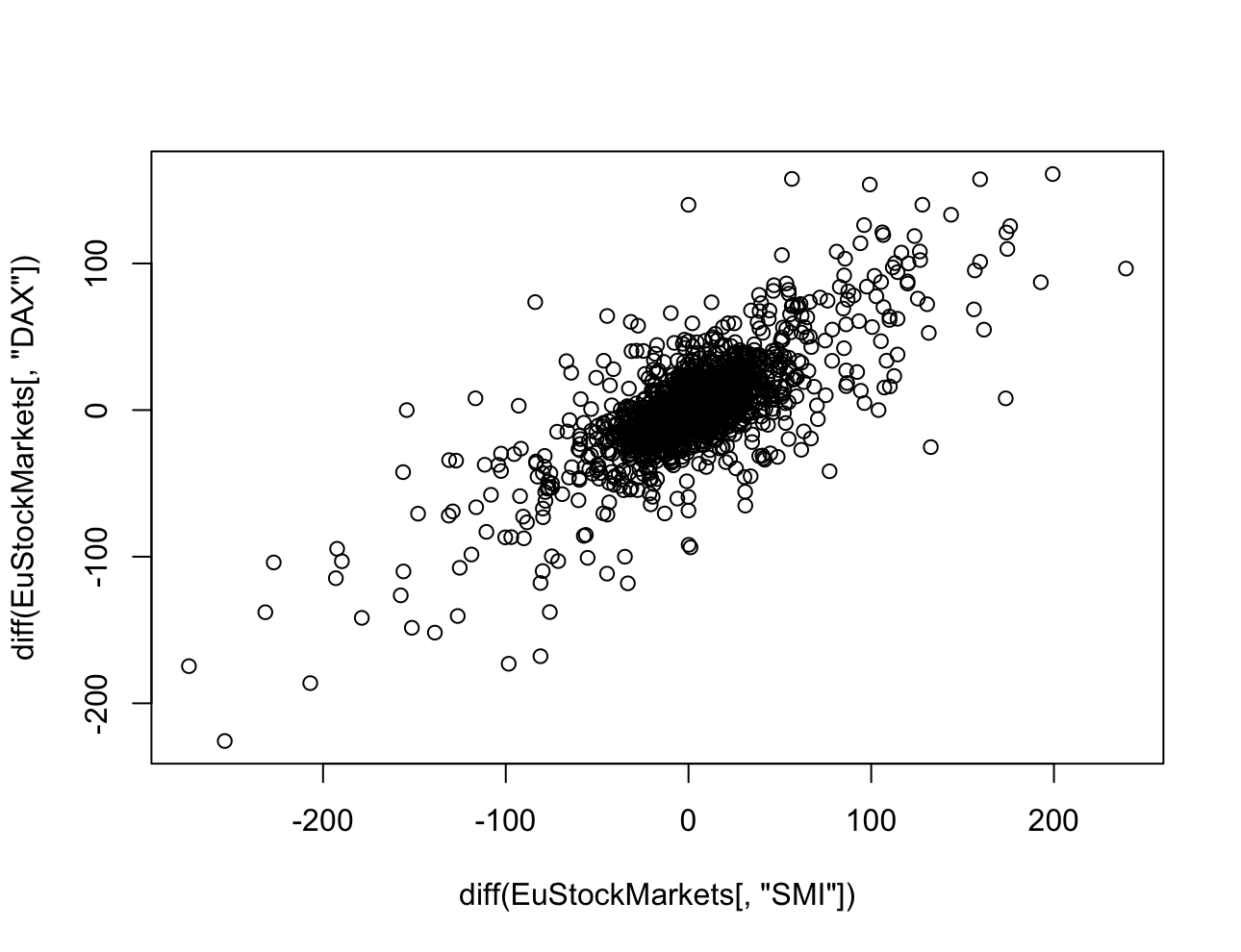
산점도도 마찬가지로 시간에 따른 서로 다른 두 주식의 가치와 차분된 결과로 본 일일 가치 변동을 확인했다.
원래의 데이터를 통해 봤을 땐 DAX와 SMI가 매우 강한 상관관계를 가지고 있는 것 처럼 보인다.
하지만 차분된 결과는 그렇게까지 강한 상관관계를 가지고 있지 않다.
이전에서 말한 것과 같이 시계열 데이터의 추세를 추가 작업없이 그대로 확인해 판단하는 것은 큰 오류를 낳는다.
그렇다고 해서 무작정 같은 시점의 차분한 결과끼리 두 변수의 상관관계를 비교하는 것 또한 옳지 않다.
실제 데이터를 탐색하는 목적과 배경을 생각해본다면 같은 시점의 두 주가를 비교하는 것은 의미가 없다.
다시 말해 시간상 먼저 알게 된 한 주가의 변동으로 나중의 다른 주가의 변동을 예측하는 것이 탐색의 목적에 부합하는 것이다.
아래 코드를 통해 한 주가의 시점을 1만큼 당기고 차분한 후 그 상관관계를 살펴보자.
> plot(lag(diff(EuStockMarkets[,"SMI"]), 1), diff(EuStockMarkets[,"DAX"]))
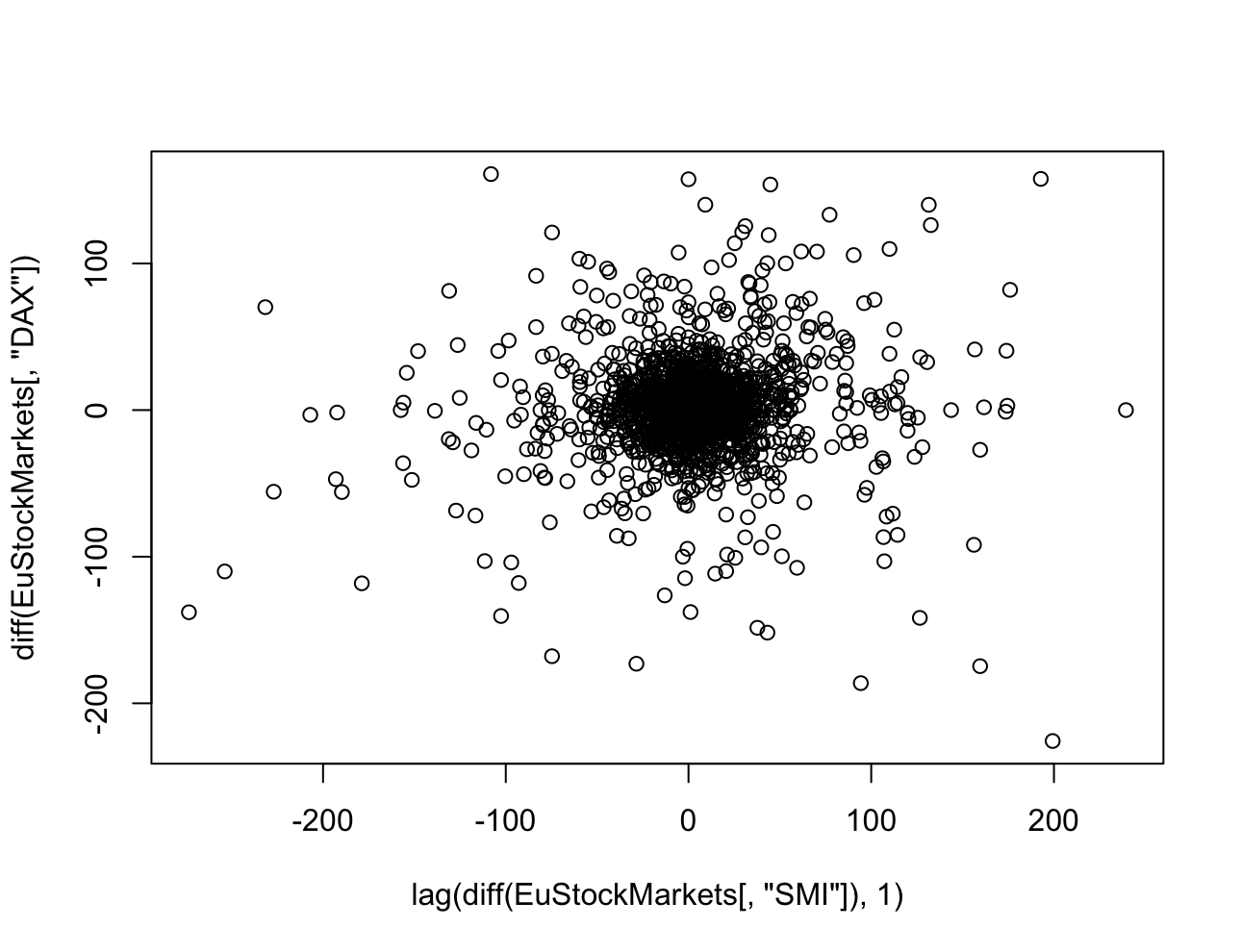
이렇게 한 결과, 두 주가 간의 상관관계는 사실상 없어졌음을 확인할 수 있다.
2. 시계열 분류의 개념과 기법
시계열 데이터를 탐색하는데 있어 비시계열 데이터와 달리 고려해야 할 사항들이 있다.
- 정상성 Stationary : 시계열이 안정성(stable)한지, 아니면 지속적인 변화를 반영하는지를 평가한 정도
- 자체 상관 Self Correlation : 시계열 자체로 연관성이 있는지와 그 시계열 내부의 역동성
- 허위 상관 Spurious Correlation : 상관 관계가 허위가 되는 것으로 상관관계와 인과관계가 다름
2-1. 정상성
정상성을 지닌 정상 시계열은 안정적인 통계적 속성, 즉 안정된 평균과 분산을 가진다.
반대로 비정상성을 가진 시계열은 평균값이 시간에 따라 변화하거나 최고점과 최저점의 간격, 즉 분산이 변화, 또는 계절성을 지니는 등과 같은 특성을 가진다.
직관적인 특성 뿐만 아니라 그 정상성을 판단하는데 사용되는 검정 방식이 있다.
대표적인 검정은 디키-플러(ADF, Augmented Dickey Fuller) 검정이 있다.
정상성의 통계적 검정은 단위근 (unit root)의 존재로 판단할 수 있고 특성 방정식의 해가 1인지를 통해 판단하다. 즉, 단위근이 있는 선형 시계열은 비정상이다.
ADF는 시계열에 단위근이 존재한다는 귀무가설을 상정하고 그 검정결과의 유의도에 근거해 기각 여부를 결정한다.
정상성과 그 검정에 대한 개념적 내용은 아래 "금융 파이썬 쿡북"의 내용을 통해 자세히 다루었다.
https://needmorecaffeine.tistory.com/25
시계열 정상성 검정 & 교정
"금융 파이썬 쿡북 Ch3. 시계열 모델링 "의 내용을 기반으로 작성하였습니다. (실습 깃헙) 1. 정상성 정상성(stationary) 시계열이란 평균, 분산, 공분산 등의 통계적 속성이 시간에 대해 일정한 시계
needmorecaffeine.tistory.com
2-2. Rolling Window (이동평균)
먼저 롤링 윈도를 통해 평활화하고 이 평활화된 결과로 노이즈가 많은 데이터의 추세를 찾거나 선형적인 동작이 단순한 노이즈인지를 판단할 수 있다.
> plot(x, type = 'l', lwd = 1)
> lines(filter(x, mn(5)), col = 2, lwd = 3, lty = 2)
> lines(filter(x, mn(50)), col = 3, lwd = 3, lty = 3)
위에서 사용한 filter는 데이터의 linear transformation이므로 일차결합한 함수를 원치 않는 경우 zoo 패키지의 rollapply 함수를 사용한다.
아래 f1과 f2는 좌측, 우측 정렬의 차이를 가지며, 좌측 정렬은 특정 시점에서부터 결정한 window 사이즈만큼의 미래 사건의 최소값을, 우측 정렬은 반대로 과거 사건의 최솟값을 정의했다.
> f1 <- rollapply(zoo(x), 20, function(w) min(w), align = "left", partial = TRUE)
> f2 <- rollapply(zoo(x), 20, function(w) min(w), align = "right", partial = TRUE)
> plot(x, lwd = 1, type = 'l')
> lines(f1, col = 2, lwd = 3, lty = 2)
> lines(f2, col = 3, lwd = 3, lty = 3)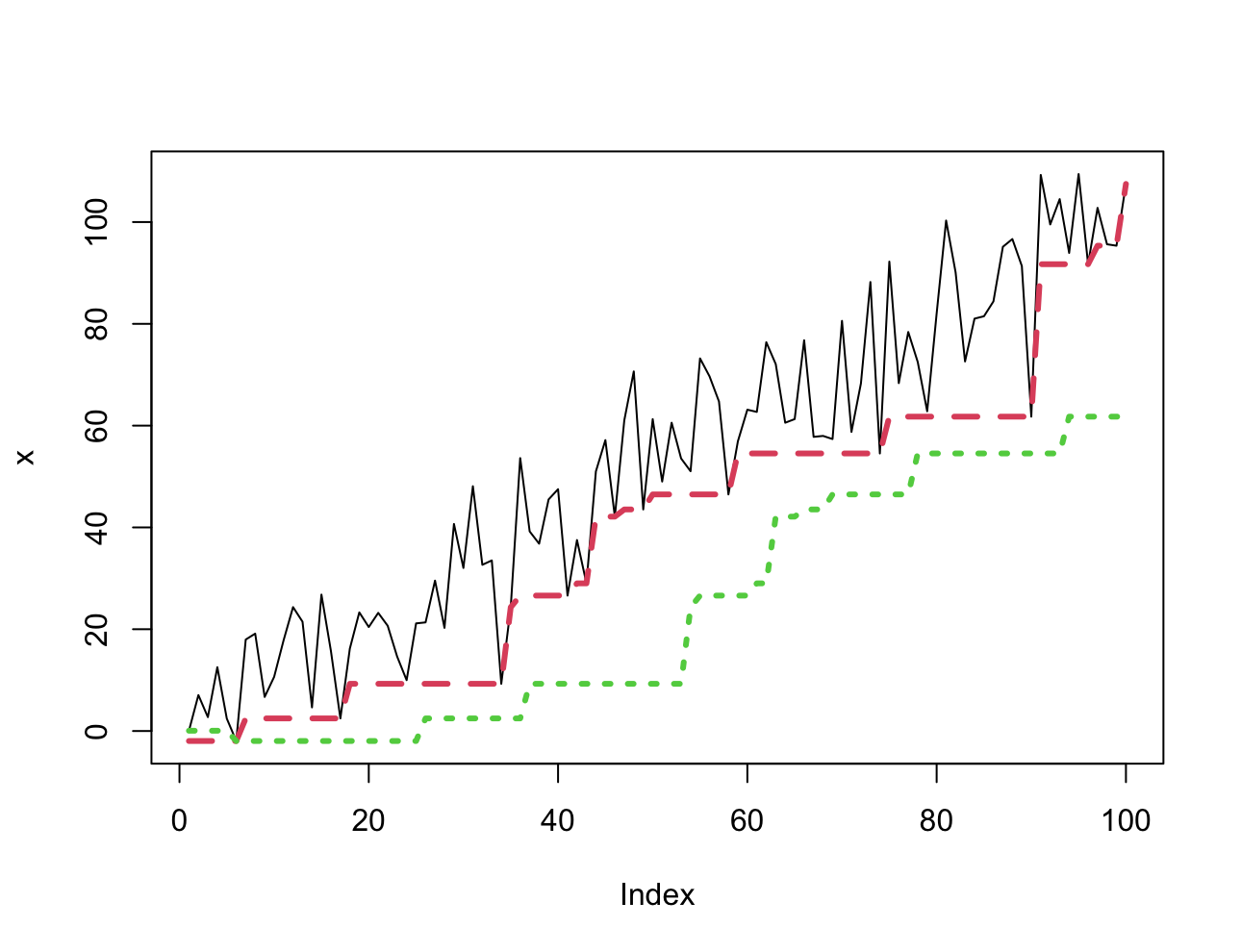
2-3. Expanding Window (누적 평균)
확장 윈도우는 롤링 윈도우보다 덜 보편적으로 사용되는데, 그 이유는 확정 윈도우를 사용하기에 적합한 경우가 제한적이기 때문이다.
확장 윈도우는 시간에 따라 크게 변화하는 것이 아닌 안정적인 요약 통게를 가질 경우, 즉 정상성을 가질 경우에만 의미가 있다.
확장 윈도우는 설정한 최소 크기의 사이즈로 탐색을 시작하지만 시계열이 진행함에 따라 주어진 시간 동안 모든 데이터를 포함할 수 있을 때까지 확장한다는 특성이 있다.
다시 정리하자면 롤링 윈도우는 특정 window width를 유지한 채 단위시간별로 이동하며 분석하지만 확장 윈도우는 처음 시작을 고정해 시간의 흐름에 따라 신규 데이터까지 누적해 분석한다는 차이가 있다.
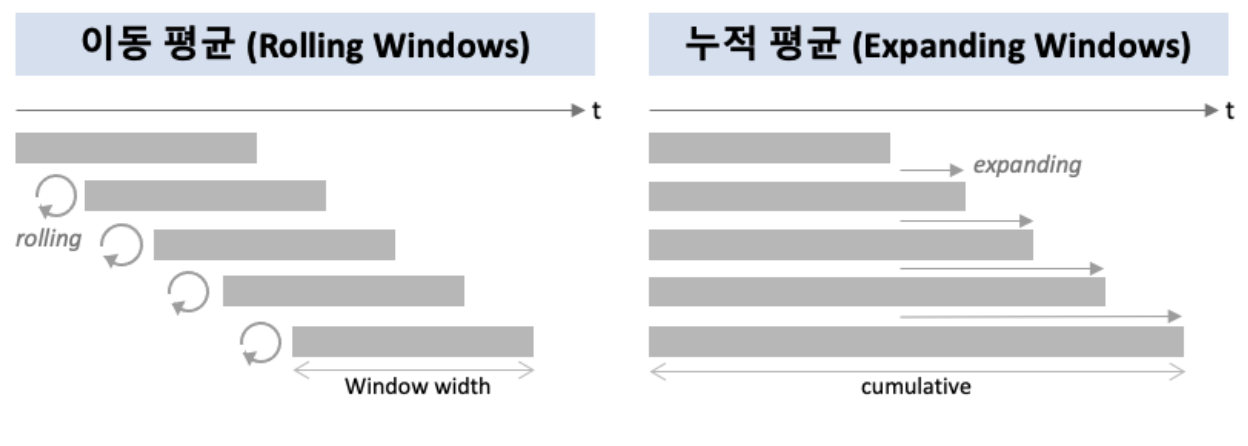
확장 윈도우는 누적 function으로 쉽게 구현 가능하고 아래는 누적 최댓값, 누적 평균값을 살펴보는 코드이다.
> plot(x, type = 'l', lwd = 1)
> lines(cummax(x), col = 2, lwd = 3, lty = 2)
> lines(cumsum(x)/1:length(x), col = 3, lwd = 3, lty = 2)
2-4. ACF와 PACF
앞서 언급한 ACF(Auto Correlation function), 자기상관함수는 시차에 따른 일련의 자기상관을 의미한다.
ACF는 시차가 커질수록 0에 가까워지고 정상성을 가진 시계열은 상대적으로 빠르게 0으로 수렴하나 비정상 시계열은 천천히 감소한다는 특징이 있다.
ACF는 일반 correlation을 구하는 방식과 동일하게 계산된다. Yt와 Yt+k 사이의 ACF를 구하는 식이다.
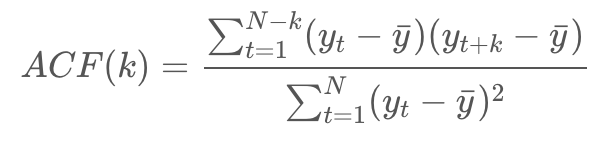
PACF(Partial Auto Correlation function)는 편자기상관함수로 시차가 다른 두 시계열 데이터 간의 순수한 상호 연관성이다.
위를 기준으로 하면 Yt와 Yt-k 간의 순수한 상관관계로 두 시점 사이의 모든 Yt-1, Yt-2 .... Yt-k+1의 영향은 제거된다.

파이썬으로 기반한 실습 내용은 다음 포스팅에서 확인할 수 있다.
https://needmorecaffeine.tistory.com/25
시계열 정상성 검정 & 교정
"금융 파이썬 쿡북 Ch3. 시계열 모델링 "의 내용을 기반으로 작성하였습니다. (실습 깃헙) 1. 정상성 정상성(stationary) 시계열이란 평균, 분산, 공분산 등의 통계적 속성이 시간에 대해 일정한 시계
needmorecaffeine.tistory.com
Ref
- Oreilly "실전시계열 분석" 3장
- https://zephyrus1111.tistory.com/169
[시계열 분석] 9. (Augmented) Dickey-Fuller Test(검정) with Python
이번 포스팅에서는 단위근 검정을 위한 대표적인 방법으로 Dickey-Fuller Test(검정)과 이를 확장한 Augmented Dickey Fuller Test(검정)에 대한 내용을 알아본다. 또한 Python(파이썬)을 이용하여 (Augmented) Dickey
zephyrus1111.tistory.com
'Time Series Analysis' 카테고리의 다른 글
| Facebook Prophet 논문 리뷰 (0) | 2023.05.15 |
|---|---|
| 시계열 통계모델 2 [이론] - ARCH / GARCH 모형 (0) | 2023.03.30 |
| 시계열 통계모델 2 [이론] - ARIMA / SARIMA / VAR 모형 (0) | 2023.03.20 |
| 시계열 통계모델 1 [이론] - Exponential Smoothing / Holt-Winter / AR / MA (0) | 2023.03.13 |
| 누락된 시계열 데이터 (1) | 2023.03.07 |