
"금융 파이썬 쿡북 Ch3. 시계열 모델링 "의 내용을 기반으로 작성하였습니다. (실습 깃헙)
1. 정상성
정상성(stationary) 시계열이란 평균, 분산, 공분산 등의 통계적 속성이 시간에 대해 일정한 시계열을 의미한다.
이런 정상성은 미래에 대한 모델링과 예측을 정확하게 해주므로 시계열에서의 바람직한 특성이다.
반대로 비정상성 데이터의 몇가지 단점은 다음과 같다.
- 모델의 분산이 잘못 지정될 수 있다.
- 모델의 적합화를 악화시킨다.
- 데이터의 시간 - 의존성이라는 귀중한 패턴을 활용할 수 없다.
2. 정상성 검정
정상성 검정을 위해서는 아래 세가지 방법을 활용 및 구현하였다.
데이터는 이전 '시계열 분해' 에서 사용한 데이터와 동일하다.
https://needmorecaffeine.tistory.com/24
시계열 분해
"금융 파이썬 쿡북 Ch3. 시계열 모델링 "의 내용을 기반으로 작성하였습니다. (실습 깃헙) 1. 시계열 분해 시계열 분해의 목표는 시계열을 여러 구성 요소로 나워 데이터에 대한 이해를 높이는 것
needmorecaffeine.tistory.com
2-1. ADF 검정 (Augmented Dickey-Fuller)
ADF 검정에 대한 통계적 설명은 다음 링크를 참고하였다.
https://zephyrus1111.tistory.com/169
[시계열 분석] 9. (Augmented) Dickey-Fuller Test(검정) with Python
이번 포스팅에서는 단위근 검정을 위한 대표적인 방법으로 Dickey-Fuller Test(검정)과 이를 확장한 Augmented Dickey Fuller Test(검정)에 대한 내용을 알아본다. 또한 Python(파이썬)을 이용하여 (Augmented) Dickey
zephyrus1111.tistory.com
# ADF (Augmented Dickey Fuller) 검정
def adf_test(x) :
indices = ['Test Statistics', 'p-value', '# of Lags Used', '# of Observations Used']
# AIC = 고려된 지연 수(lags)를 AIC(Akaike Information Criterion) 기반 자동 선택
adf_test = adfuller(x, autolag = 'AIC')
results = pd.Series(adf_test[0:4], index = indices)
for key, value in adf_test[4].items() :
results[f'Critical Value ({key})'] = value
return results
adf_test(df.price)
ADF 검정의 귀무가설은 '시계열이 정상성이 아니다' 이고 귀무가설을 채택하므로 해당 계열은 정상성이 아니라는 결론을 내릴 수 있다.
2-2. KPSS 검정 (Kwiatkowski-Phillips-Schmidt-Shin)
KPSS에 대한 통계적 설명은 다음 링크를 참고하였다.
https://syj9700.tistory.com/30
시계열 검정 (자기상관 검정, 단위근 검정, 정상성 검정)
1. 계열상관 검정 시계열의 자기상관(=계열상관) 여부를 파악하는 방법에 대해 알아보자. 이는 잔차를 시각화하거나 통계적인 검정을 통해 확인할 수 있다. 본 포스팅에서는 통계적 검정을 이용
syj9700.tistory.com
# KPSS (Kwiatkowski-Phillips-Schmidt-Shin) 검정
# c = 시계열이 level 정상성이라는 귀무가설
# ct = 시게열이 trend 정상성이라는 귀무가설 (계열에서 trend를 제거하면 level 정상성이 됨)
def kpss_test(x, h0_type = 'c') :
indices = ['Test Statistics', 'p-value', '# of Lags Used']
kpss_test = kpss(x, regression = h0_type)
results = pd.Series(kpss_test[0:3], index = indices)
for key, value in kpss_test[3].items() :
results[f'Critical Value ({key})'] = value
return results
kpss_test(df.price)
귀무가설은 '시계열이 정상성이다'로 귀무가설을 기각하므로 해당 계열은 정상성이 아니라는 결론을 내릴 수 있다.
2-3. 부분 자기 상관 함수 PACF / ACF 검정 (Partial Autocorrelation Function)
자기 상관에 대한 통계적 설명은 다음 링크를 참고하였다.
https://datalabbit.tistory.com/112
[시계열분석] 자기상관함수(AutoCovariance Function; ACF)
안녕하십니까, 간토끼입니다. 이번 포스팅에서는 시계열자료의 특성을 파악할 수 있는 중요한 지표 중 하나인 자기상관함수(AutoCovariance Function; ACF)에 대해 다뤄보도록 하겠습니다. 항상 강조하
datalabbit.tistory.com
# (부분) 자기 상관 함수 PACF / ACF (Partial Autocorrelation Function)
N_LAGS = 40
SIGNIFICANCE_LEVLE = 0.05
fig, ax = plt.subplots(2,1)
plot_acf(df.price, ax = ax[0], lags = N_LAGS, alpha = SIGNIFICANCE_LEVLE)
plot_pacf(df.price, ax = ax[1], lags = N_LAGS, alpha = SIGNIFICANCE_LEVLE)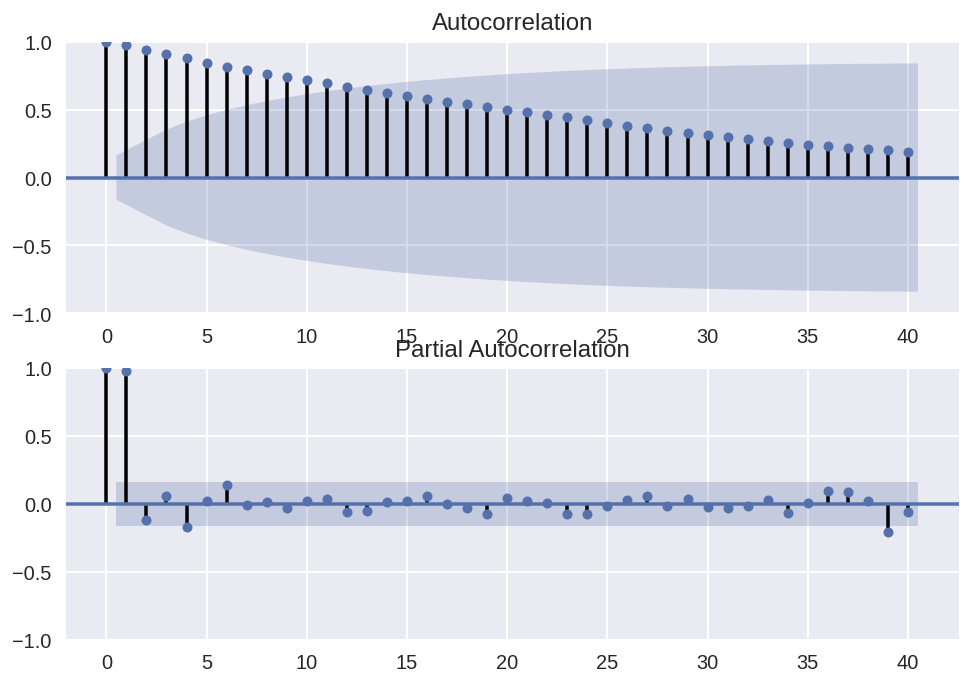
그래프를 보면 유의한 자기 상관이 있음을 알 수 있다. (선택된 5% 유의 수준에 해당하는 95% 신뢰 구간 이상)
또한 PACF에서는 지연 1과 4에서 유의한 자기 상관이 있다.
위 세가지 방식을 통해 정상성을 검증했을 때의 결론은 모두 월별 금 가격 시계열은 비정상성을 띈다는 것이다.
3. 비정상성 교정
이런 비정상성을 교정하기 위한 방식으로 다음 세가지 변환을 취할 수 있다.
사용한 데이터는 이전 데이터와 동일하다.
3-1. 디플레이션
말 그대로 소비자 물가지수 CPI를 사용해 인플레이션을 반영하는 것이다.
CPI 데이터를 로드하는 방식부터 인플레이션을 보정한 가격을 구하는 것은 다음 과정을 통해 이루어진다.
!pip install cpi
from datetime import date
# CPI 데이터를 통해 미국달러의 인플레이션 반영 (노동 통계청의 CPI-U)
import cpi
cpi.update()# 디플레이션 : 소비자 물가지수를 사용해 인플레이션을 반영
DEFL_DATE = date(2011, 12, 31)
df['dt_index'] = df.index.map(lambda x : x.to_pydatetime().date())
# cpi.inflate : x.price = 조정하려는 달러 값 / x.dt_index = 달러값의 날짜(위에서 변환 완료) / DEFL_DATE = 이 날짜로 인플레이션 조정
df['price_deflated'] = df.apply(lambda x : cpi.inflate(x.price, x.dt_index, DEFL_DATE), axis = 1)
print(df)
df[['price', 'price_deflated']].plot(title = 'Gold Price (deflated)')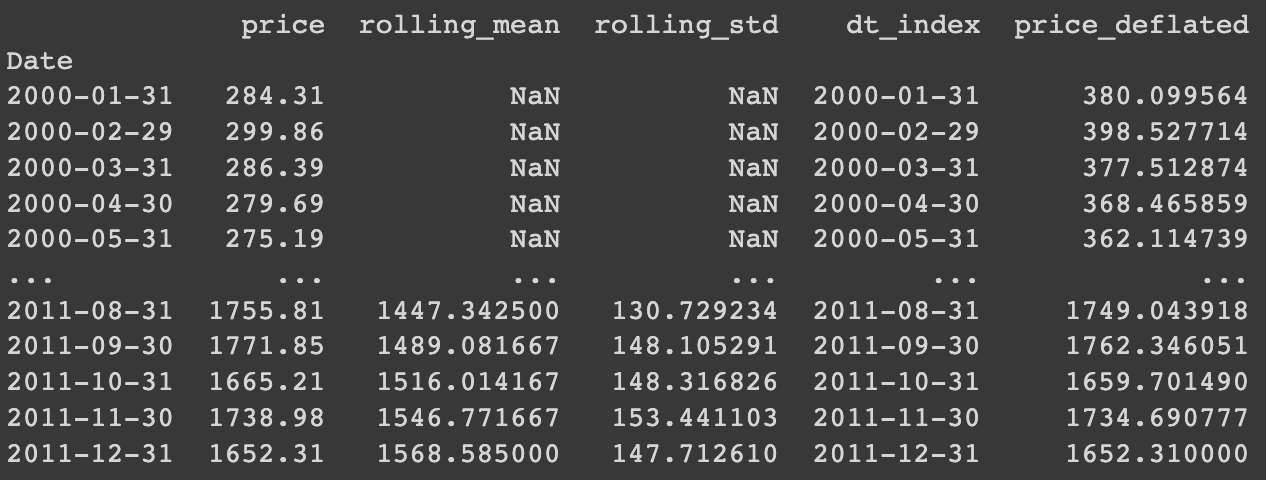
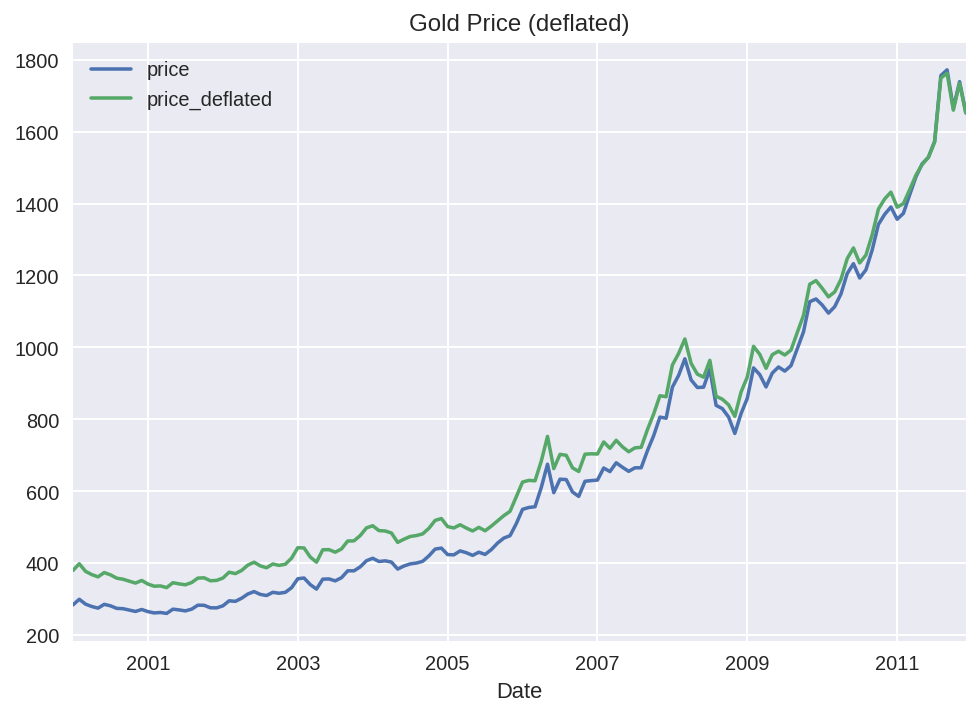
3-2. 자연로그
지수 추세를 로그를 씌워 선형에 가깝게 만드는 방식이다.
시계열을 자연로그를 사용해 디플레이션 시키고 이동 척도에 따라 도식화한다.
# 자연 로그(지수 추세를 선형에 가깝게 만든다)를 사용해 디플레이션시키고 이동 척도에 따라 도식화
WINDOW = 12
selected_columns = ['price_log', 'rolling_mean_log', 'rolling_std_log']
df['price_log'] = np.log(df.price_deflated)
df['rolling_mean_log'] = df.price_log.rolling(window = WINDOW).mean()
df['rolling_std_log'] = df.price_log.rolling(window = WINDOW).std()
df[selected_columns].plot(title = 'Gold Price (logged)')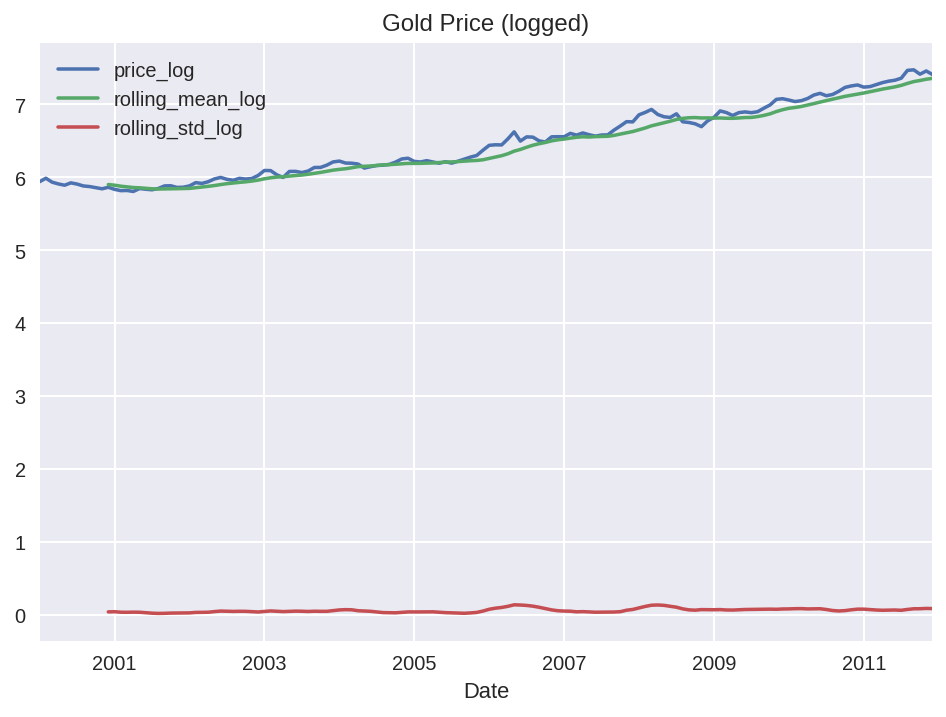
지수의 추세가 선형에 가까워 졌음을 알 수 있다.
우선 여기까지 수행한 두가지 방식에 대해 비정상성이 정상성으로 변환됐는지 확인해보자.
아래 코드는 이전에 정상성을 검증했던 방식을 하나의 function에 담은 것이다.
# 하나의 함수
def test_autocorrelation(x, n_lags=40, alpha=0.05, h0_type='c'):
adf_results = adf_test(x)
kpss_results = kpss_test(x, h0_type=h0_type)
print('ADF test statistic: {:.2f} (p-val: {:.2f})'.format(adf_results['Test Statistics'],
adf_results['p-value']))
print('KPSS test statistic: {:.2f} (p-val: {:.2f})'.format(kpss_results['Test Statistics'],
kpss_results['p-value']))
fig, ax = plt.subplots(2, figsize=(16, 8))
plot_acf(x, ax=ax[0], lags=n_lags, alpha=alpha)
plot_pacf(x, ax=ax[1], lags=n_lags, alpha=alpha)
return fig# 정상성이 되었는지 확인
test_autocorrelation(df.price_log)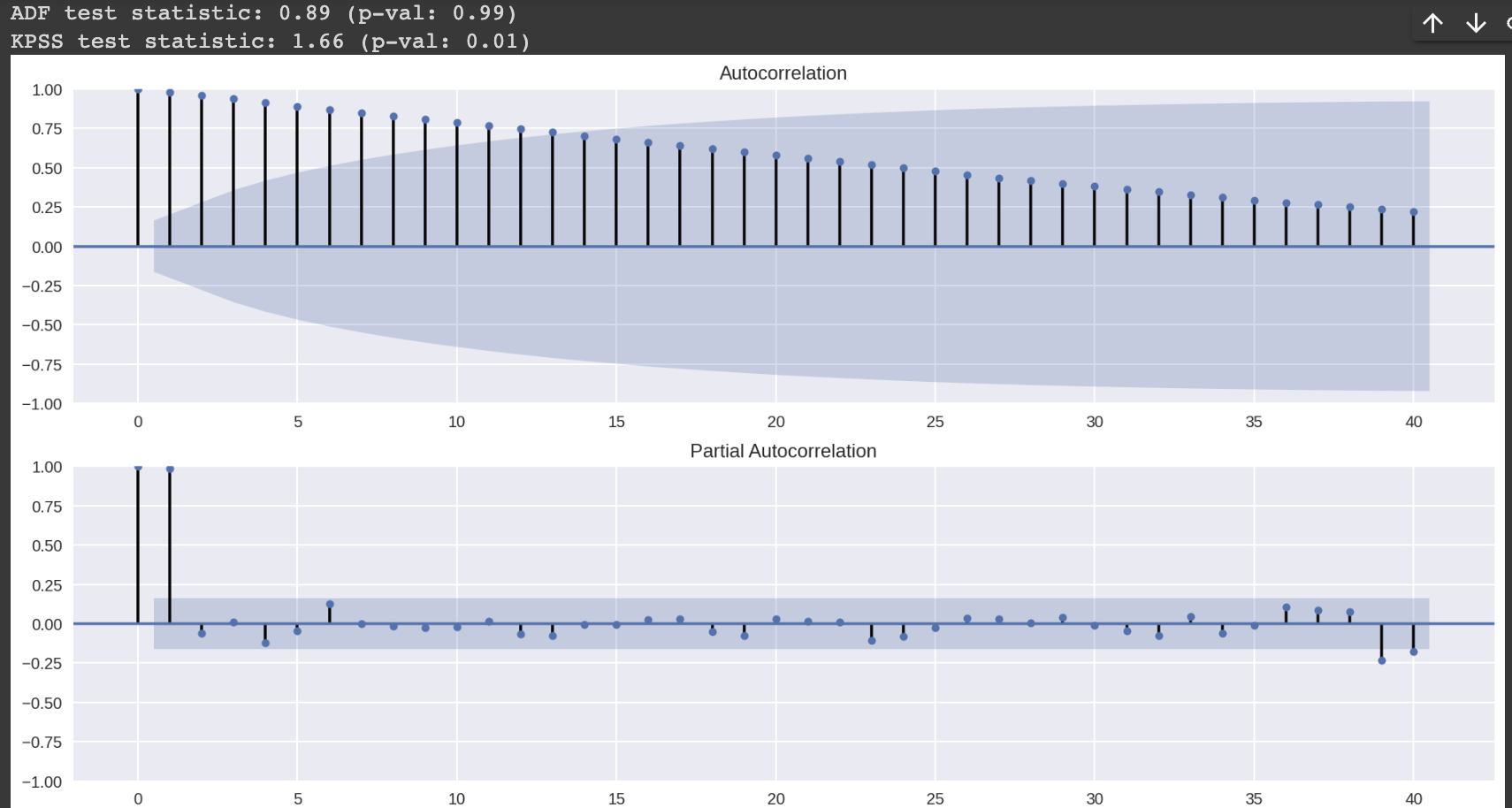
통계적 수치와 시각화 결과를 보았을 때, 아직 정상성으로 변환되지 않았음을 확인할 수 있다.
3-3. 차분 (Differentiation)
현 관측값과 지연값 사이의 차분을 반영한다.
# 차분 : 현 관측값과 지연 값 사이의 차이
selected_columns = ['price_log_diff', 'roll_mean_log_diff',
'roll_std_log_diff']
# 시간 t와 시간 t-1의 값의 차이
df['price_log_diff'] = df.price_log.diff(1)
df['roll_mean_log_diff'] = df.price_log_diff.rolling(WINDOW).mean()
df['roll_std_log_diff'] = df.price_log_diff.rolling(WINDOW).std()
df[selected_columns].plot(title='Gold Price (1st differences)')
plt.tight_layout()
plt.show()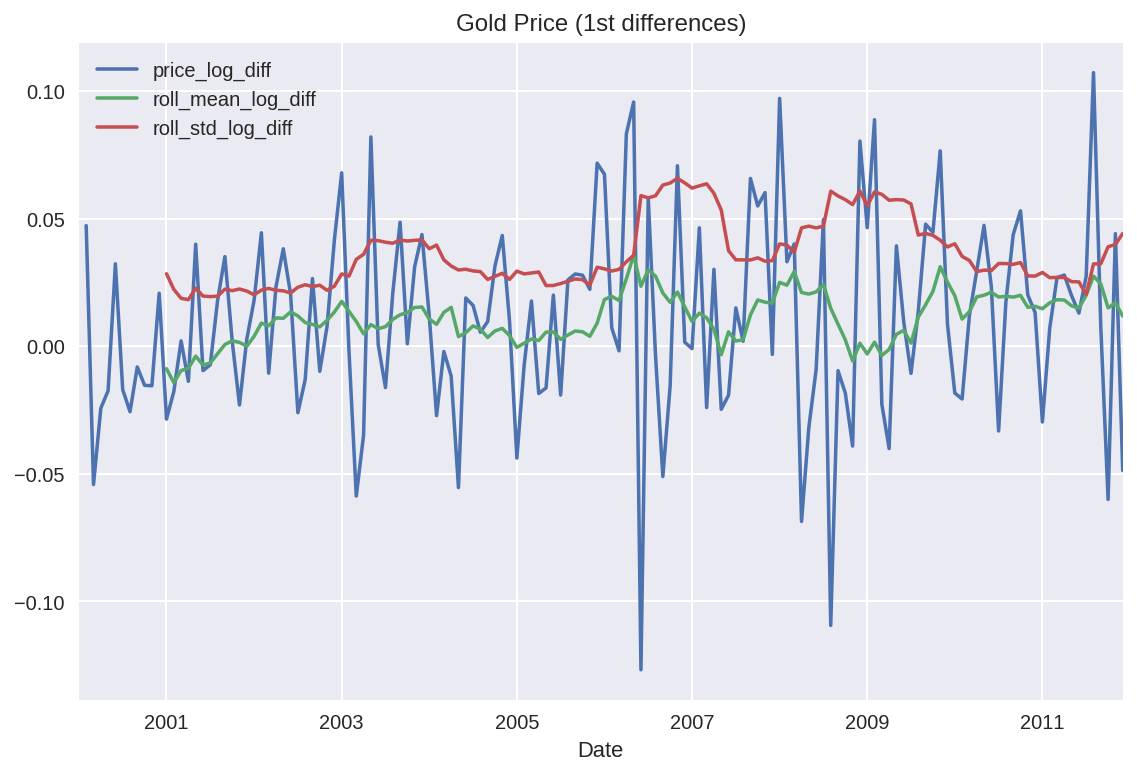
시각화된 결과만 봤을 땐 대략 일정한 분산을 갖고 0 주위에서 진동하는데 정상성으로 변환된 것 처럼 보인다.
여기까지 작업한 내용으로 정상성으로 변환되었는지 다시 한번 확인해보자.
# 정상성이 되었는지 확인
test_autocorrelation(df.price_log_diff.dropna())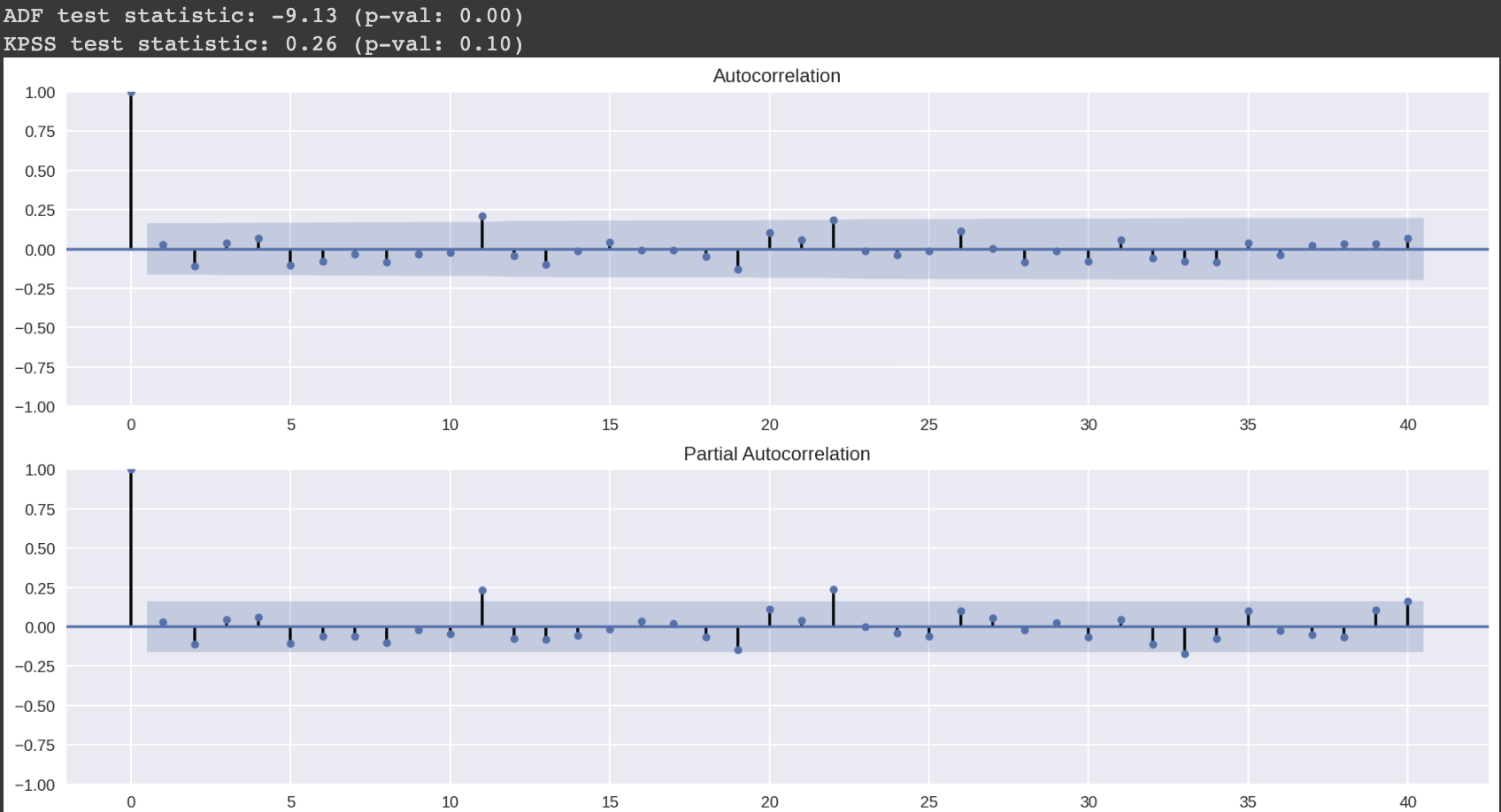
1차 차분을 적용한 후에 5% 유의 수준에서 정상상태가 됐다.
시각화 결과도 지연 11과 22를 제외하고는 모두 정상 상태인데 이는 일종의 계절성을 나타내거나 단순 잘못된 신호일 수 있다.
해당 지점은 유의 수준 5%로 검정한 것 처럼 자기 상관이나 부분 자기 상관이 없더라도 신뢰구간을 벗어날 수 있기에 등장한 지점이라고 할 수 있다.
4. 계절적 패턴이 나타날 경우 해결책
더 나아가 계절성이 나타날 경우 어떻게 핸들하지에 대해서도 다뤄보자.
사용한 데이터를 봤을 때 계절성은 찾기 힘들었지만 만일 존재한다고 할 때 다음의 방법으로 계절성을 제거할 수 있다.
- 차분으로 조정 : 1차 차분을 사용하는 대신 월별 데이터에 연간 계절성이 있는 경우, 더 높은 차수를 사용한다.(ex. diff(12))
- 모델링을 통한 조정
- 계절성을 직접 모델링한 후 계열에서 제거한다. seasonal_decompose나 다른 고급 가종 분해 알고리즘을 사용해 계절성분을 추출할 수 있다.
- 이 경우 Additive 모델을 사용할 때 계절 성분을 뺴야하고 모형이 Multiplicative일 경우 나눠야 한다.
- 또 다른 방식으로는 np.polyfit()을 사용해 선택한 시계열에 최적 차수의 다항식을 적합화한 다음, 원래 시계열에서 이를 빼낸다.
- 박스 콕스 변환
- 다른 지수 변환 함수를 결합해 분포를 정규 분포와 더 유사하게 만든다.
- scipy의 boxcox를 사용하면 가장 적합한 lambda 매개 변수 값을 자동으로 찾을 수 있다.
- 단 이때 시계열의 모든 값이 양수여야 한다. 1차 차분 혹은 변환을 통해 시계열에 음수 값이 나타나는 경우에 사용해서는 안된다.
- pmdarima 라이브러리
- 통계검정을 사용해 정상성을 달성(계절적 정상성 제거)하기 위해 차분으로 조정하는 방식을 진행할 경우, 이 때 적용해야 할 차분의 차수를 알아낼 수 있는 두가지 함수 (ndiffs, nsdiffs)를 사용한다.
- ADF, KPSS, 필립-페론 검정을 통해 정상성을 검사할 수 있고 그에 맞는 차분의 차수를 알 수 있다.
!pip install pmdarima
from pmdarima.arima import ndiffs, nsdiffs
print(f"Suggested # of differences (ADF): {ndiffs(df.price, test='adf')}")
print(f"Suggested # of differences (KPSS): {ndiffs(df.price, test='kpss')}")
print(f"Suggested # of differences (PP): {ndiffs(df.price, test='pp')}")
- 계절적 차이 유뮤 검정
- OSCB (Osborn, Chui, Smith, Birchenhall) 과 CH (Canova-Hansen)를 통해 계절성 유뮤를 판단할 수 있다.
- 사용하고 있는 데이터는 월별 데이터 이므로 데이터의 빈도를 12로 지정한다.
# 계절적 차이 검정
# 월별로 데이터로 작업하고 있으므로 데이터의 빈도(12)를 지정
print(f"Suggested # of differences (OSCB): {nsdiffs(df.price, m=12, test='ocsb')}")
print(f"Suggested # of differences (CH): {nsdiffs(df.price, m=12, test='ch')}")
예상했던 대로 해당 데이터는 계절성이 없다고 결론지을 수 있다.
(해당 게시물 학습을 위한 임의적 설정이므로, 수익을 대변하지 않습니다.)
Ref
- 금융 파이썬 쿡북, 에릭 르윈슨.
- https://zephyrus1111.tistory.com/169
- https://syj9700.tistory.com/30
- https://datalabbit.tistory.com/112
[시계열분석] 자기상관함수(AutoCovariance Function; ACF)
안녕하십니까, 간토끼입니다. 이번 포스팅에서는 시계열자료의 특성을 파악할 수 있는 중요한 지표 중 하나인 자기상관함수(AutoCovariance Function; ACF)에 대해 다뤄보도록 하겠습니다. 항상 강조하
datalabbit.tistory.com
시계열 검정 (자기상관 검정, 단위근 검정, 정상성 검정)
1. 계열상관 검정 시계열의 자기상관(=계열상관) 여부를 파악하는 방법에 대해 알아보자. 이는 잔차를 시각화하거나 통계적인 검정을 통해 확인할 수 있다. 본 포스팅에서는 통계적 검정을 이용
syj9700.tistory.com
[시계열 분석] 9. (Augmented) Dickey-Fuller Test(검정) with Python
이번 포스팅에서는 단위근 검정을 위한 대표적인 방법으로 Dickey-Fuller Test(검정)과 이를 확장한 Augmented Dickey Fuller Test(검정)에 대한 내용을 알아본다. 또한 Python(파이썬)을 이용하여 (Augmented) Dickey
zephyrus1111.tistory.com
'Advance Deep Learning > [Quant] 금융 파이썬 쿡북' 카테고리의 다른 글
| 시계열 모델링 - ARIMA (0) | 2023.02.07 |
|---|---|
| 시계열 모델링 - 지수 평활법 (0) | 2023.02.03 |
| 시계열 분해 (0) | 2023.02.02 |
| 볼린저 밴드 계산과 매수/매도 전략 테스트 (1) | 2023.01.30 |
| 단순이동평균(SMA)를 기반으로 전략 백테스팅 (0) | 2023.01.30 |