해당 포스팅은 Sean J Tay, Benjamin Letham의 'Forecasting at Scale' 논문을 기반으로 작성되었습니다.
위의 논문을 리뷰한 내용은 다음과 같다.
1. Intro
페이스북에서 근무하는 두 저자는 business time series 분석 도구, 즉 Prophet 패키지를 만들었는데 많은 사람들이 쓸 수 있는 "scale"한 분석 도구를 만드는 것이 목적이었다고 한다.
실제 많은 시계열 관련 분석이 Prophet을 통해 이뤄지고 있다.

많은 auto화 된 패키지가 그렇듯 위 analyst-in-loop의 하단의 automated 파트는 자동화된 툴을 사용하는 것을 추구한다.
자동화된 패키지 구성을 위해서 뿐만 아니라 시계열에서는 다양한 요소들이 고려되어야 한다.
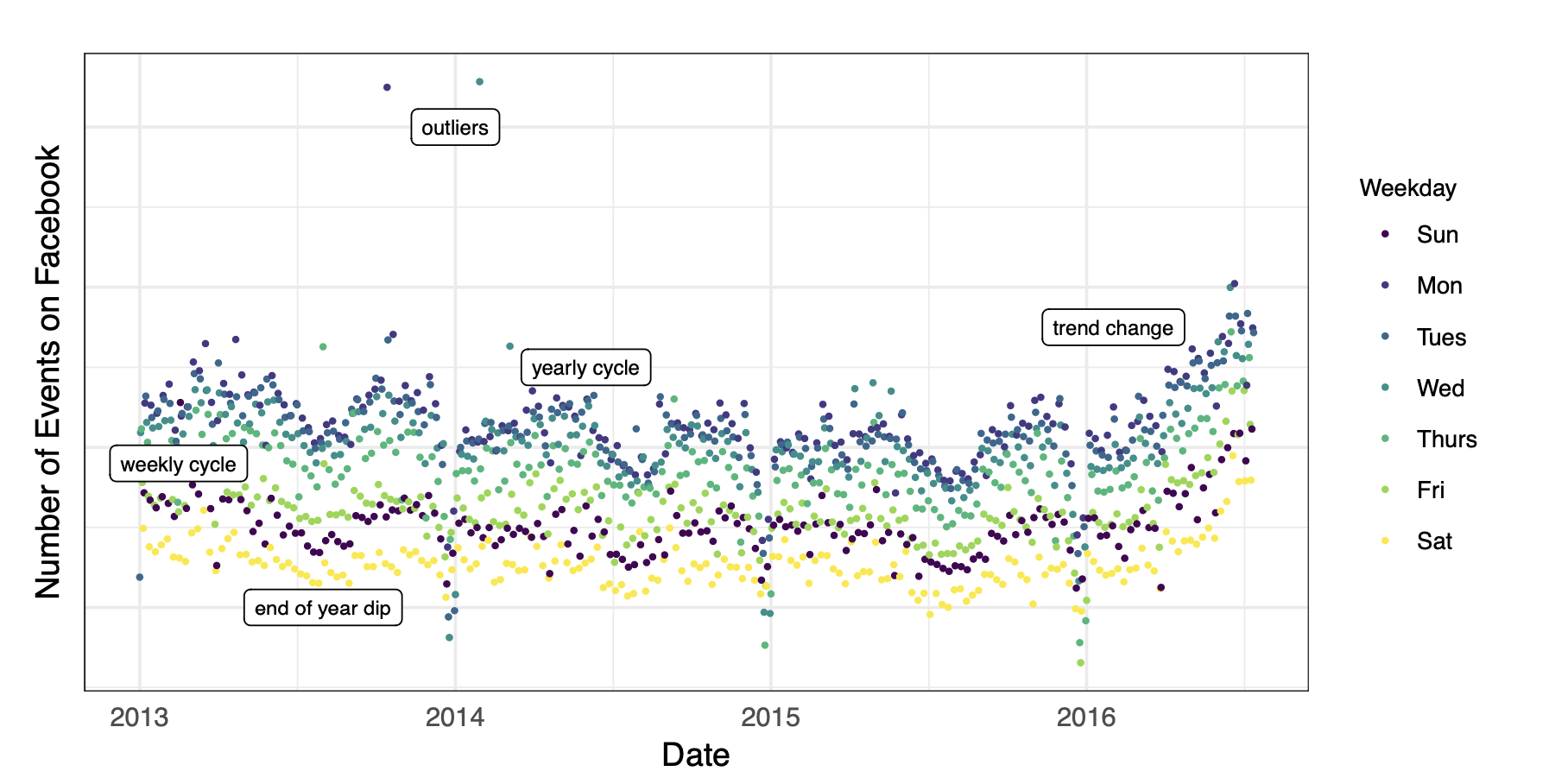
실제 페이스북의 evemt 발생 시계열 데이터를 보면 연도별, 요일별 cycle과 trend의 변화, outlier 등 많은 요소들이 복합적으로 작용되고 있고 제대로 된 시계열 분석은 이것들을 모두 고려할 수 있어야 한다.
그렇다면 prophet 등장 이전의 전통적인 시계열 분석 기법들은 이것들을 잘 고려하였을까?
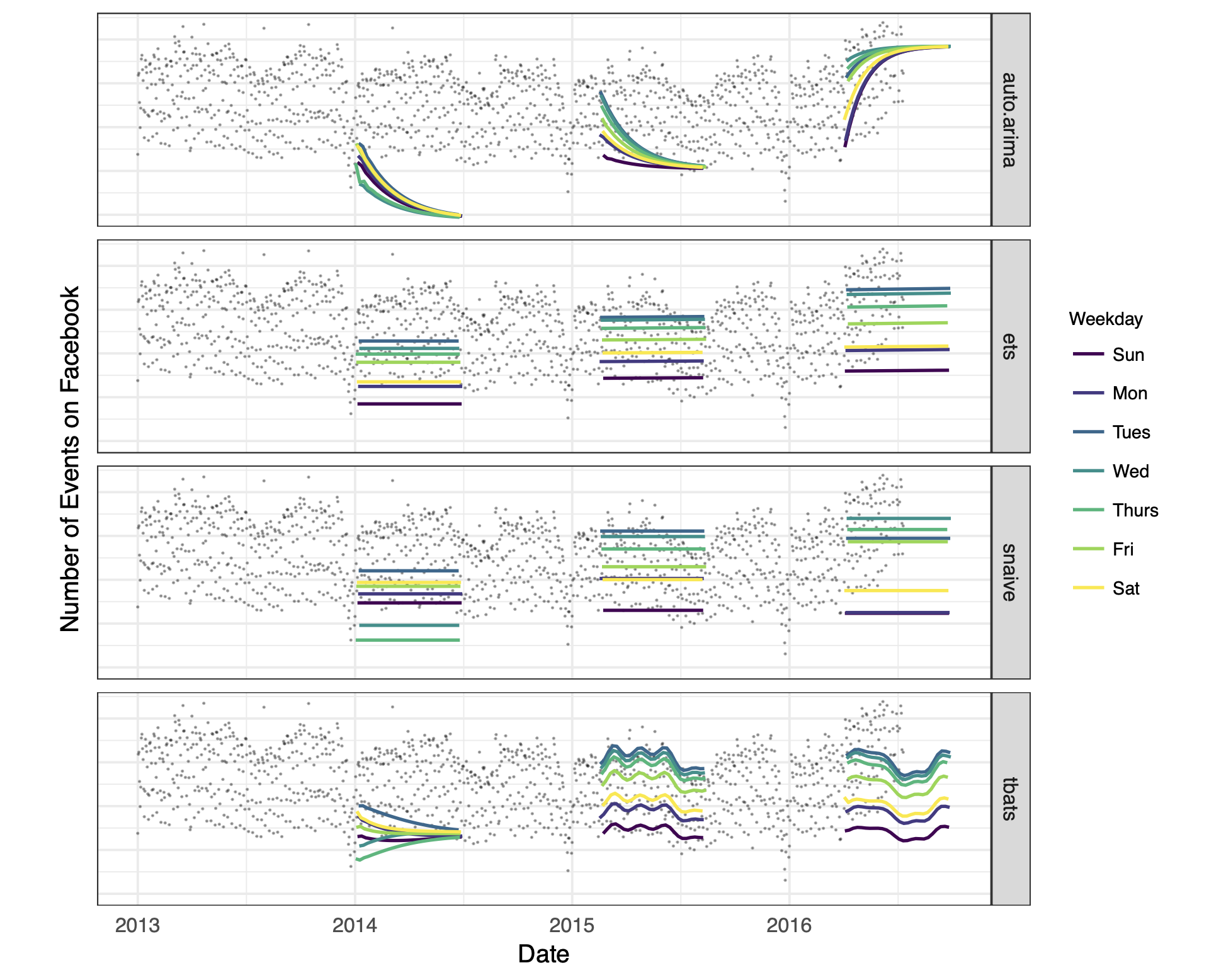
위부터 auto arima, 지수평활법, seasonal naive, tbats 기법인데 auto arima는 trend를 일부 잘 따라가지만 나머지 기법들은 거의 직적 모향으로 예측하고 있음을 알 수 있다. 이는 분석 및 예측이 잘못되고 있음을 의미한다.
2. 구성
Prophet은 Harvey&Peters 가 제안한 다음의 요소를 반영하였다.
$y(t)$ = $g(t) + s(t) + h(t) + e_{t}$
- $g(t)$ : trend function which models non-periodic changes in the value of the time series
- $s(t)$ : represents periodic changes (e.g., weekly and yearly seasonality)
- $h(t)$ : effects of holidays which occur on potentially irregular schedules over one or more days
- $e(t)$ : error term
위 구성은 Generalized Additive Model (GAM)의 구조와 유사하다.
이런 가법적(additive) 방식은 가승적(multiplicative)모델과 달리 새로운 시계열에 대해 다시 모델을 쉽게 훈련할 수 있을며 여러 기간에 대해 예측할 수 있다는 점 등의 장점을 가진다.
요소마다 살펴보면 다음과 같다.
2-1. $g(t)$, Trend
페이스북에서 사용하는 trend model은 두가지가 있는데 saturating growth model과 piecewise linear model이다.
saturating growth model 부터 살펴보자.
Growth Forecasting이란 특정 시계열 데이터와 관련된 Population, 즉 페이스북에서는 잠재적인 사용자가 어떻게 그 수가 성정해왔고 이후 어떻게 성장할 것인지를 예측하는 것이다.
이를 nonlinear growth that saturates at a carrying capacity라고 부르고 있다.
페이스북에서의 carrying capacity는 인터넷 접속이 가능한 사용자로 설정하고 있고 다음과 같이 $g(t)$를 정의하고 있다.
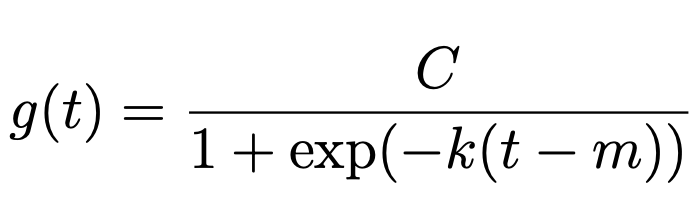
- C = carrying capacity
- k = growth rate
- m = offset parameter
다만 여기서 C, k는 계속 변화하기 때문에 이도 time t에 따른 변화를 반영해야 한다.
이 때 change point라는 요소가 추가되는데 이 change point들을 명시하여 tred에 따른 변화를 감지하고자 한다.
- $S_{j}$ : changepoint 지점
- $\delta_{j}$ : $S_{j}$의 변화율
- $\delta$ : $\delta_{j}$로 이루어진 벡터
이 때 base rate인 k를 기준으로 j 시점부터 $t > S_{j}$ 시점까지의 $\delta_{j}$를 더해준다.

좀 더 간편하게 $a_{j}(t)$를 다음과 같이 정의하고

time t에서의 변화율을 $k + a(t)^{t}\delta$ 로 바꿔 표현 가능하며 k를 adjust했다면 그에 따라 m도 adjust해야 하므로 최종적인 변화율은 다음과 같다.

위 사항들을 모두 반영한 최종 piece wise growht model은 다음과 같다.
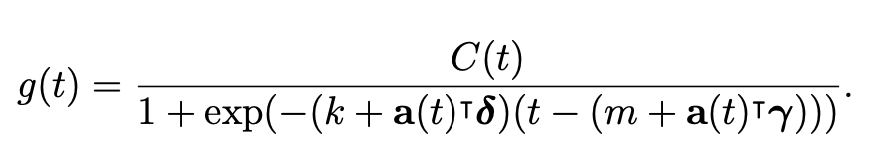
논문에서 C(t)의 구성에 대해 명확히 명시하지 않았는데 이는 적용되는 도메인과 목적에 맞춰 함수를 제작해야 한다고 말하고 있다.
이 때 change point $S_{j}$는 분석가에 의해 사전 정의될 수 있는데 이 change point는 과거의 데이터를 살펴보고 과거 데이터에서 발생한 changepoint과 동일한 주기로 발생한다고 가정해 $\delta_{j}$가 $Laplace(0, \tau)$ 를 따라는다고 가정한다.
2-2. Seasonality
Seasonality는 다음과 같이 푸리에 급수를 이용해 정의된다.
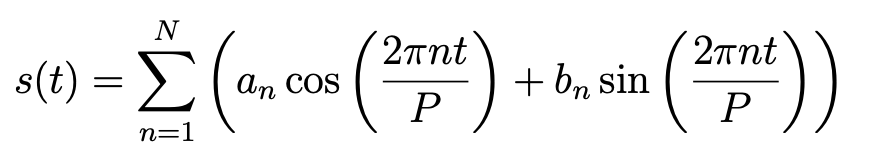
여기에서 P는 시계열 데이터가 가지는 규칙적인 period이다.
년 단위는 P = 365.25, 주 단위는 P = 7 로 설정해 사용한다.
이 때의 a, b 2N개의 파라미터 $\beta = [a_{1}, b_{1}, \cdots, a_{N}, b_{N}]^{T}$ 는
아래의 seasonality vector로 이루어진 matrix 추정되고
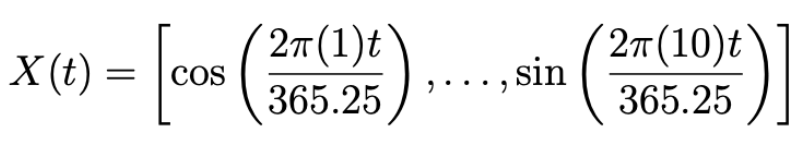
최종적으로 seasonal component는 다음과 같이 정의된다.
$s(t) = X(t)\beat$
또한 N 값의 설정도 고려되어야 하는데 여기서 N은 seasonality의 low-pass filter 기능을 하고 N 값이 크면 seasonal pattern이 빠르게 변하게 된다.
N 값은 통상적으로 년 단위는 10, 주 단위는 3으로 설정하는 것이 가장 좋다고 알려져 있다.
2-3. Holidays and Events
휴일과 여러 이벤트들은 산업 현장의 시계열에 많은 영향을 준다.
미국의 추수감사절, 한국의 추석과 같은 휴일은 특정 품목과 도메인에 확연한 영향을 주는 것이 그 예이다.
이 때 나라마다 그 휴일이 다르기 때문에 분석가가 상황에 맞추어 custom list를 제작하여 각 나라별 holiday 컬럼은 반영해 예측을 진행한다.
각각의 holiday를 $D_{i}$로 명시하고 holiday i 동안의 t와 각 휴일에 할당되는 파라미터를 $k_{i}$ 라고 하였을 때 다음의 matrix를 만들 수 있다.
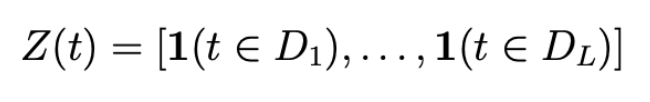
seasonailty와 유사하게 다음과 같의 정의된다.

3. Fitting & Evaluating
지정된 time 길이에 맞춰 fitting을 하였다면 이 모델이 잘 작동하는지 확인해야 한다.
그 기준인 accuracy는 다음과 같이 측정된다.
- H = 예측을 진행하는 기간
- $\hat{y}(t|T)$ = time T까지의 정보를 이용해 time t에 대해 예측한 값
- $d(y, y') = |y - y'|$

이 때 다음의 error term은 몇가지 가정을 가진다.
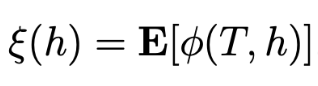
- 연속된 time에서는 유사한 mistake이 생기는 것을 가정했기에 h 동안 error는 locally smooth해야 한다.
- 시간이 지날수록, 예측력은 떨어진다.
이 때 논문에서는 error를 측정하기 위해 Simulated Historical Forecast 방법은 제안한다.
시계열 이외의 데이터는 데이터를 셔플하고 error를 반복적으로 측정하는 방식으로 error를 산출하는데 시계열 데이터는 셔플 자체가 되지 않는다.
따라서 시간 순을 유지한 채 지정된 window size로 데이터들을 자르고 자른 데이터 각각을 fitting된 model로 예측해 여러 error들이 어느 지점으로 수렴되는지 파악한다.
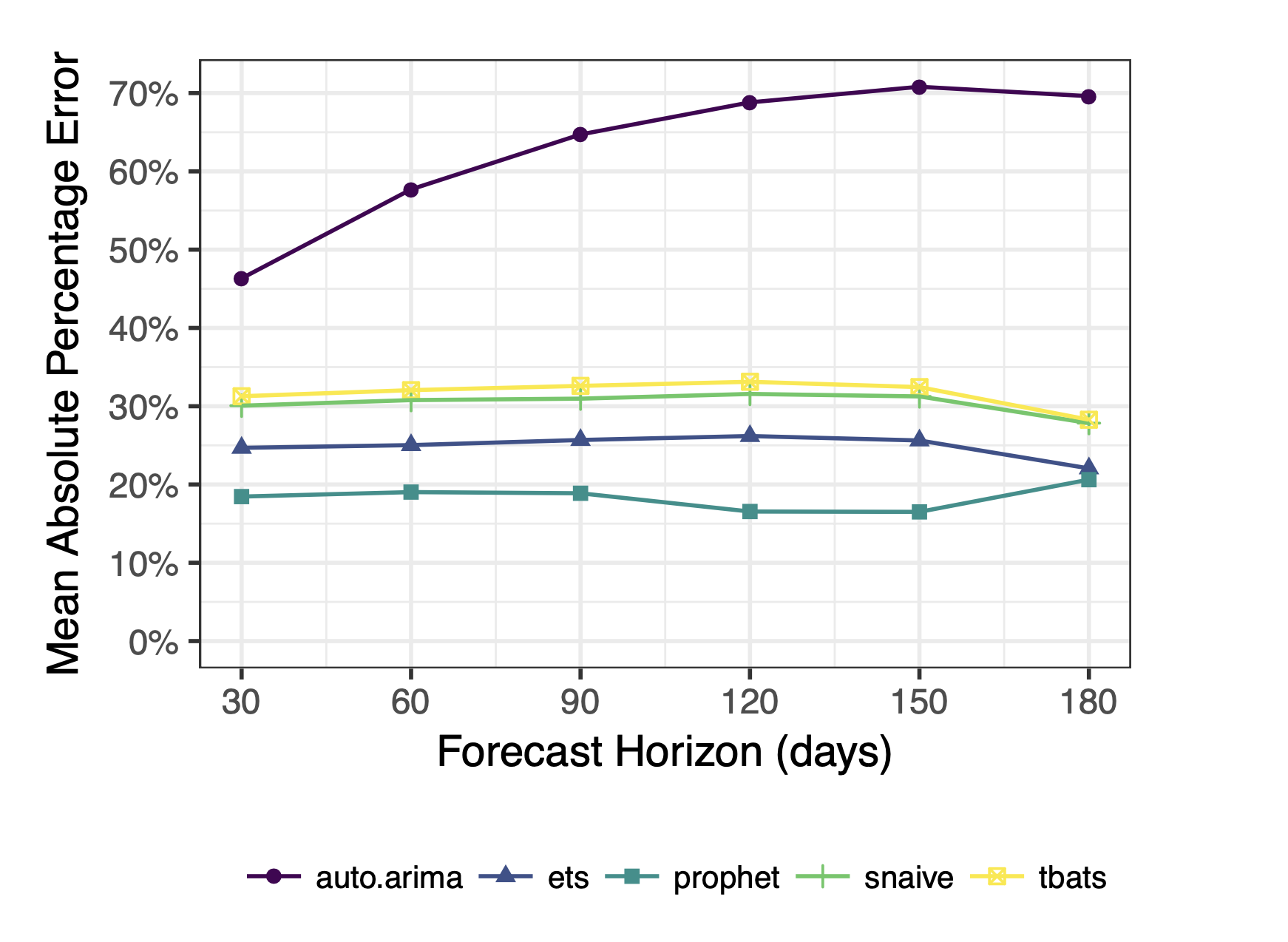
MAPE를 기준으로 최종 실험한 결과는 위와 같다.
Prophet이 일정하게 MAPE가 다른 모델에 비해 낮은 것을 확인할 수 있다.
Ref
https://peerj.com/preprints/3190.pdf
'Time Series Analysis' 카테고리의 다른 글
| 시계열 통계모델 2 [이론] - ARCH / GARCH 모형 (0) | 2023.03.30 |
|---|---|
| 시계열 통계모델 2 [이론] - ARIMA / SARIMA / VAR 모형 (0) | 2023.03.20 |
| 시계열 통계모델 1 [이론] - Exponential Smoothing / Holt-Winter / AR / MA (0) | 2023.03.13 |
| 시계열 데이터 EDA (0) | 2023.03.09 |
| 누락된 시계열 데이터 (1) | 2023.03.07 |