
"금융 파이썬 쿡북 Ch3. 시계열 모델링 "의 내용을 기반으로 작성하였습니다. (실습 깃헙)
1. 지수 평활법 (Exponential Smoothing)
지수 평활법은 비정상 데이터(trend, seasonality를 띄는 데이터)에 사용하며 예측은 과거 관측값의 가중 평균을 사용한다는 점에서 지수 이동 평균과 유사하게 작동한다.
이 모델은 시간이 지나면서 가중치가 기하급수적으로 작아짐에 따라 최근 관측에 더 중점을 둔다.
이번 포스팅에서는 단순 지수 평활과 홀트 모델과 그 확장 모델에 대해 다뤄보겠다.
1-2. 단순 지수 평활 (SES, SImple Exponential Smoothing)
지수 평활의 가장 기본적인 모델이다. 이 모델은 고려 중인 시계열이 trend나 seasonality를 띄지 않을 경우와 데이터가 얼마 없는 시계열의 경우에 잘 작동한다.
이 모델은 아래 수식돠 같이 0과 1 사이의 값을 갖는 smoothing 매개 변수 alpha로 매개 변수화된다. 이 alpha의 값이 클수록 최근 관측값에 더 많은 가중치가 적용된다.
- alpha = 0 : 미래 예측은 과거 데이터의 평균과 같음
- alpha = 1 : 모든 예측은 훈련 데이터의 마지막 관측값과 동일한 값을 가짐
- 예측함수는 수평선이다 = 시간의 범위와 관계 없이 모든 예측 기간에 대해 1개의 값(=마지막 level 값)을 가짐
- 따라서 trend나 seasonality가 없는 시계열에만 적합함.

구글 주가 데이터를 통해 예측하는 과정까지 구현해보자.
!pip install yfinance
import matplotlib.pyplot as plt
import warnings
plt.style.use('seaborn')
# plt.style.use('seaborn-colorblind') #alternative
#plt.rcParams['figure.figsize'] = [4, 2.5]
#plt.rcParams['figure.dpi'] = 100
warnings.simplefilter(action='ignore', category=FutureWarning)
import seaborn as sns
plt.set_cmap('cubehelix')
sns.set_palette('cubehelix')
COLORS = [plt.cm.cubehelix(x) for x in [0.1, 0.3, 0.5, 0.7]]
import pandas as pd
import numpy as np
import yfinance as yf
from datetime import date
from statsmodels.tsa.holtwinters import (ExponentialSmoothing,
SimpleExpSmoothing,
Holt)df = yf.download('GOOG',
start='2010-01-01',
end='2018-12-31',
progress=False)
print(f'Downloaded {df.shape[0]} rows of data.')
# 월별 주기로 집계
goog = df.resample('M').last().rename(columns = {'Adj Close' : 'adj_close'}).adj_close
train_indices = goog.index.year < 2018
goog_train = goog[train_indices]
goog_test = goog[~train_indices]
test_length = len(goog_test)
goog.plot(title = 'Google Stock Price' )
# SES (Simple Exponential Smoothing) / 단순 지수 평활
ses_1 = SimpleExpSmoothing(goog_train).fit(smoothing_level=0.2)
# test_length = 예측하고자 하는 기간
ses_forecast_1 = ses_1.forecast(test_length)
ses_2 = SimpleExpSmoothing(goog_train).fit(smoothing_level=0.5)
ses_forecast_2 = ses_2.forecast(test_length)
# smoothing level을 지정하는 것이 아닌 최적 적합화(잔차 제곱합의 최소화) 하도록 함
ses_3 = SimpleExpSmoothing(goog_train).fit()
alpha = ses_3.model.params['smoothing_level']
ses_forecast_3 = ses_3.forecast(test_length)
SimpleExponentialSmoothing과 fit 메서드를 사용해 세가지 다른 SES 모델을 적합화 했다.
위 두개의 모델은 smoothing_level을 수동으로 지정하였지만 마지막 하나의 모델은 statmodels이 최적 적합화하도록 했다.
이 때 최적 적합화는 잔차 제곱의 합계 최소화 방식으로 진행된다.
goog.plot(color=COLORS[0],
title='Simple Exponential Smoothing',
label='Actual',
legend=True)
ses_forecast_1.plot(color=COLORS[1], legend=True,
label=r'$\alpha=0.2$')
ses_1.fittedvalues.plot(color=COLORS[1])
ses_forecast_2.plot(color=COLORS[2], legend=True,
label=r'$\alpha=0.5$')
ses_2.fittedvalues.plot(color=COLORS[2])
ses_forecast_3.plot(color=COLORS[3], legend=True,
label=r'$\alpha={0:.4f}$'.format(alpha))
ses_3.fittedvalues.plot(color=COLORS[3])
plt.tight_layout()
plt.show()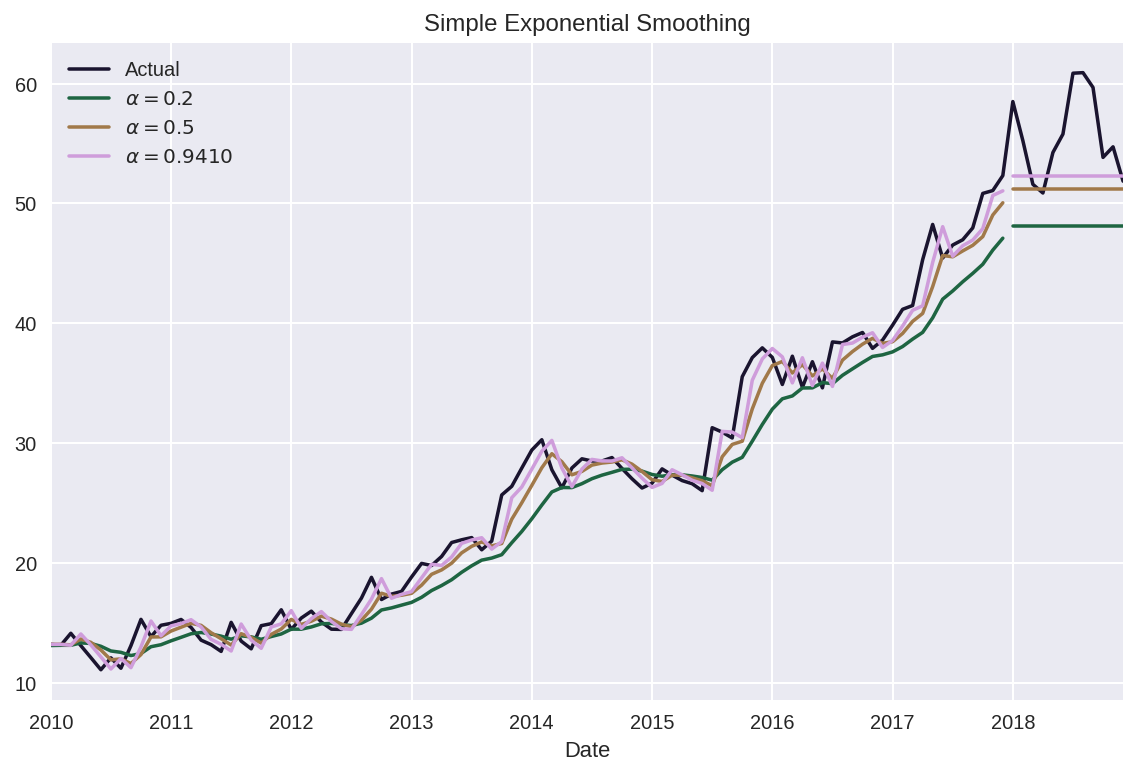
fittedvalues 메서드로 적합화된 값을 반환하고 시각화하였다.
시각화 결과, 위에서 언급한 SES 모델의 특성 (예측 결과는 수평선의 형태를 띈다)이 드러난다. 또한 최적의 alpha 값이 1에 가깝다는 사실도 알 수 있다.
1-2. Holt's Model
홀트 모델은 SES의 확장으로 tredn 구성 요소를 모델에 추가해 시계열의 추세를 고려한다.
이 모델은 데이터에 trend는 있지만 seasonality는 없는 경우에만 사용해야 한다.

이 홀트 모델의 한가지 문제점은 미래의 trend를 일정하게 여긴다는 것이고 이는 데이터가 무한대로 증가/감소할 것으로 예측한다는 것이다. 이 때문에 모델을 확장하면 감쇠 매개 변수를 추가해 trend를 완화하고 향후 trend을 일정한 값에 수렴하도록 하여 효과적인 평찬화를 진행한다. 히드만과 아사나소풀로스에 따르면 이 매개변수 값은 0.8에서 0.98 사이일 때 최적이며 이 값이 1일 경우 의도했던 감쇠효과는 없어진다.
동일한 데이터로 구현해보자.
# Holt 추세 방법
## 선형 추세 Holt
hs_1 = Holt(goog_train).fit()
hs_forecast_1 = hs_1.forecast(test_length)
## 지수 추세 Holt
hs_2 = Holt(goog_train, exponential = True).fit()
hs_forecast_2 = hs_2.forecast(test_length)
## 지수 추세 Holt + 감쇠
hs_3 = Holt(goog_train, exponential = False, damped = True).fit(damping_slope = 0.99)
hs_forecast_3 = hs_3.forecast(test_length)
기본 설정 모델의 trend는 선형이지만 exponential = True를 통해 지수 trend를, damped = True를 통해 감쇠를 추가할 수 있다.
또한 SES와 마찬가지로 fit 메서드를 통해 최적의 매개 변수의 값을 자동으로 찾는다.
goog.plot(color=COLORS[0],
title="Holt's Smoothing models",
label='Actual',
legend=True)
hs_1.fittedvalues.plot(color=COLORS[1])
hs_forecast_1.plot(color=COLORS[1], legend=True,
label='Linear trend')
hs_2.fittedvalues.plot(color=COLORS[2])
hs_forecast_2.plot(color=COLORS[2], legend=True,
label='Exponential trend')
hs_3.fittedvalues.plot(color=COLORS[3])
hs_forecast_3.plot(color=COLORS[3], legend=True,
label='Exponential trend (damped)')
plt.tight_layout()
plt.show()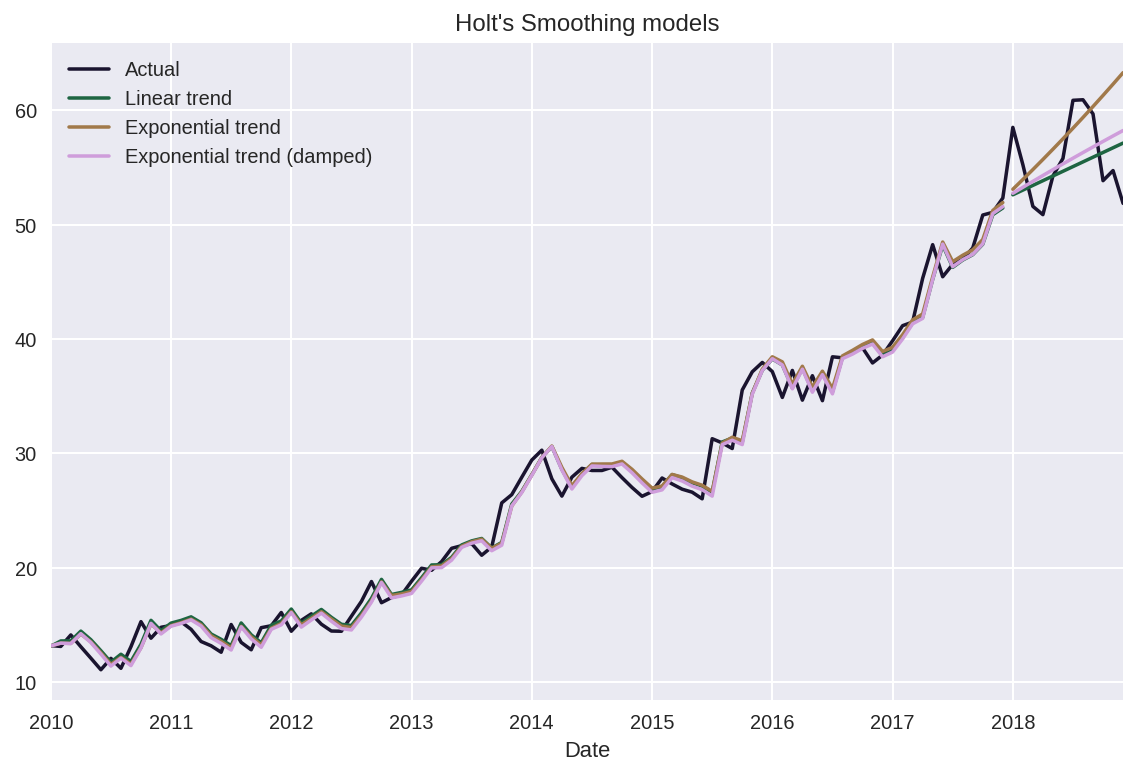
결과를 보았을 때 SES 모델은 예측값을 수평선으로 반환했지만 홀트 모델은 그렇지 않기에 trend를 조금이나마 더 잘 반영하고 있음을 알 수 있다.
1-3. Holt - Winter's Seasonal Smoothing
이는 홀트 모델의 확정법이고 seasonality도 고려할 수 있다.

# Holt-Winter's Seasonal Smoothing
SEASONAL_PERIODS = 12
# 지수 추세
hw_1 = ExponentialSmoothing(goog_train, trend = 'mul', seasonal = 'add', seasonal_periods = SEASONAL_PERIODS).fit()
hw_forecast_1 = hw_1.forecast(test_length)
# 지수 추세 + 댐핑
hw_2 = ExponentialSmoothing(goog_train, trend = 'mul', seasonal = 'add', seasonal_periods = SEASONAL_PERIODS, damped = True).fit()
hw_forecast_2 = hw_2.forecast(test_length)goog.plot(color=COLORS[0],
title="Holt-Winter's Seasonal Smoothing",
label='Actual',
legend=True)
hw_1.fittedvalues.plot(color=COLORS[1])
hw_forecast_1.plot(color=COLORS[1], legend=True,
label='Seasonal Smoothing')
phi = hw_2.model.params['damping_trend']
plot_label = f'Seasonal Smoothing (damped with $\phi={phi:.4f}$)'
hw_2.fittedvalues.plot(color=COLORS[2])
hw_forecast_2.plot(color=COLORS[2], legend=True,
label=plot_label)
plt.tight_layout()
plt.show()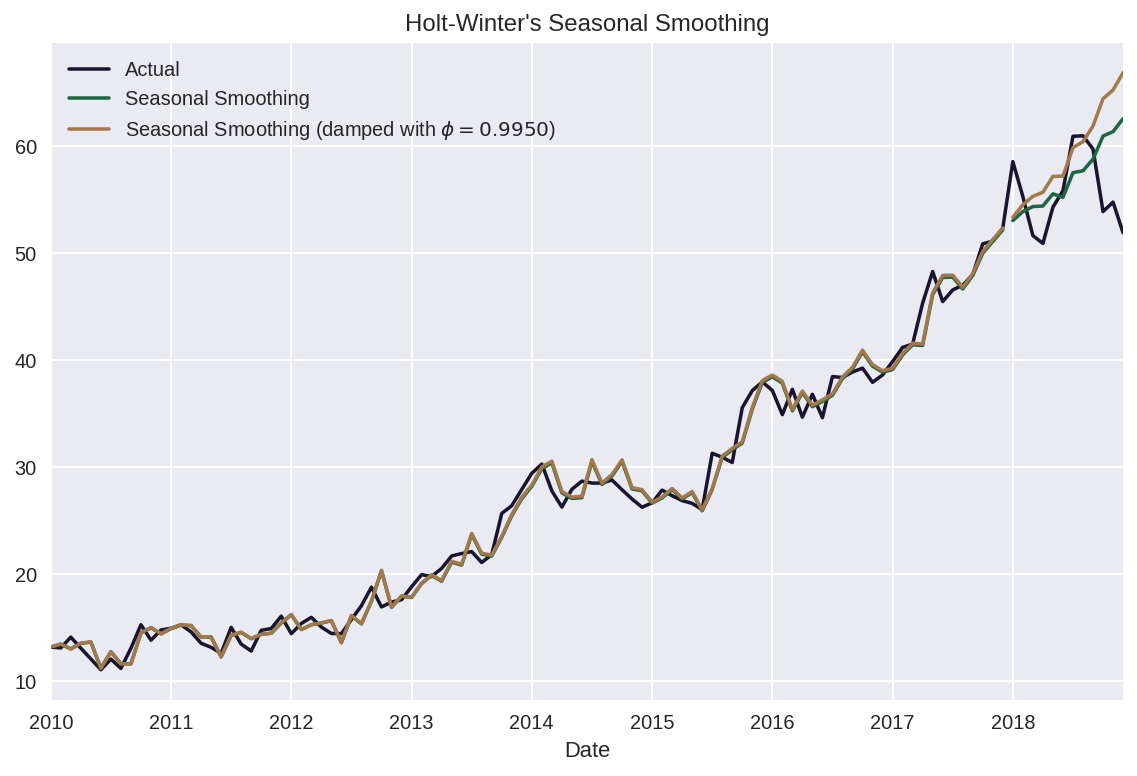
월 별 데이터를 처리하고 있으므로 SEASONAL_PERIODS=12로 설정하였다.
이전의 모델들 보다 더욱 유연하게 예측하고 있다는 것을 알 수 있다.
(해당 게시물 학습을 위한 임의적 설정이므로, 수익을 대변하지 않습니다.)
Ref
- 금융 파이썬 쿡북, 에릭 르윈슨.
- https://datalabbit.tistory.com/75
- https://icim.nims.re.kr/post/easyMath/840
[시계열분석] 단순지수평활법(Simple Exponential Smoothing Method)
안녕하십니까, 간토끼입니다. 지난 포스팅까지는 시계열자료의 추세(Trend)를 이용하여 미래의 시계열을 예측하는 추세분석에 대해서 다뤄봤습니다. 추세를 나타내는 변수 t, 혹은 t의 Polynomial Ter
datalabbit.tistory.com
'Advance Deep Learning > [Quant] 금융 파이썬 쿡북' 카테고리의 다른 글
| 시계열 모델링 - ARIMA (0) | 2023.02.07 |
|---|---|
| 시계열 정상성 검정 & 교정 (0) | 2023.02.02 |
| 시계열 분해 (0) | 2023.02.02 |
| 볼린저 밴드 계산과 매수/매도 전략 테스트 (1) | 2023.01.30 |
| 단순이동평균(SMA)를 기반으로 전략 백테스팅 (0) | 2023.01.30 |