
"금융 파이썬 쿡북 Ch3. 시계열 모델링 "의 내용을 기반으로 작성하였습니다. (실습 깃헙)
1. 시계열 분해
시계열 분해의 목표는 시계열을 여러 구성 요소로 나워 데이터에 대한 이해를 높이는 것이다.
이를 통해 모델링의 복잡성과 각 구성 요소를 정확하게 캡처하고 따랴아 하는 접근 방식에 대한 통찰력을 얻을 수 있다.
1-1. 시계열 구성 요소
이 때 언급되는 각 구성요소는 체계적과 비체계적인 두 가지 유형을 나눌 수 있다.
- 체계적 구성요소
- Level : 계열의 평균값
- Trend : 추세의 추정치, 즉 특정시점에서 연속 시점 사이의 값 변화. 시계열의 기울기와 연관됨.
- Seasonality : 단기 사이클로 반복되는 평균으로부터의 차이
- 비체계적 구성요소
- Noise : 시계열 상의 랜덤 변화
1-2. 시계열 분해에 사용되는 모델
시계열 분해에 사용되는 모델에는 Additivie(가산적), Multiplicative(승산적)로 두가지 유형이 있고 특징은 다음과 같다.
- Additive
- 모델 식 : y(t) = level + trend + seasonality + noise
- 선형 모델 : 시간에 따른 크기 변화가 일정
- trend는 선형성을 띔
- 시간 주기에 대한 동일한 빈도(높이)와 폭(너비)을 가진 선형 seasonality
- Multiplicative
- 모델 식 : y(t) = level * trend * seasonality * noise
- 비선형 모델 : 시간에 따른 크기 변화가 일정하지 않음
- 곡선이며 비선형 trend
- 시간 주기에 대해 증가/감소하는 빈도와 폭을 가지는 비선형 seasonality
- 특정 변환을 이용해 trend / seasonality를 선형으로 만들어 Additive 모델을 사용할 수 있음 (지수 증가 >> 로그값 취하기)
아래 그림으로 더 설명하자면 Additive의 경우 데이터의 진폭이 일정하지만, Multiplicative의 경우 데이터의 진폭이 점점 증가 / 감소한다. 이 두가지 유형을 잘 구분하지 않고 시계열 분해를 수행하게 될 경우, residual을 제대로 분리하지 못하게 된다.

(Ref : https://hyperconnect.github.io/2020/03/09/prophet-package.html)
2. 구현
2-1. Statsmodel 라이브러리를 사용해 시계열 분해
퀀들에서 다운로드한 월별 금 가격을 시계열 분해 해보자.
!pip install quandl
import quandl
import pandas as pd
from statsmodels.tsa.seasonal import seasonal_decompose# 금 시세 다운
df = quandl.get(dataset = 'WGC/GOLD_MONAVG_USD',
start_date = '2000-01-01',
end_date = '2011-12-31')
df
df.rename(columns = {'Value' : 'price'}, inplace = True)
# 월별 마지막 값만 가져오기
df = df.resample('M').last()# 이동 평균과 표준 편차 추가
WINDOW_SIZE = 12
df['rolling_mean'] = df.price.rolling(window = WINDOW_SIZE).mean()
df['rolling_std'] = df.price.rolling(window = WINDOW_SIZE).std()
df.plot(title = 'Gold Price')
시각화 해본 결과 이동평균에 비선형 성장 패턴이 있고, 이동 표준편차가 시간이 지남에 따라 증가함을 알 수 있다.
따라서 Mulitplicative 모델을 사용한다.
# 계절성 분해
decomposition_results = seasonal_decompose(df.price, model = 'multiplicative')
decomposition_results.plot().suptitle('Mutliplicative Decomposition', fontsize = 10)
앞서 언급한 구성 요소별로 시각화된 결과를 볼 수 있다.
이 때 분해가 적절하게 되었는지 확인하기 위해서는 랜덤 성분을 살펴볼 수 있다. 랜덤 성분에 식별 가능한 특정 패턴이 없다면 분해가 적절히 되었다고 판단할 수 있다.
2-2. 페이스북의 Prophet을 사용해 시계열 분해
페이스북의 Prophet은 서로 다른 시간 단위(일, 주, 월 등) 패턴의 조합으로 전체 trend를 나타낼 수 있다.
특히 Prophet은 변환점(행동의 급격한 변화), 휴일 등을 고려하는 등의 고급 기능을 가지고 있으며 시계열의 미래 값을 불확실성 수준을 나타내는 신뢰구간과 함께 예측할 수 있다는 장점이 있다.
2000~2005년 일별 금 가격에 적용해보자.
!pip install prophet
import seaborn as sns
from prophet import Prophet# 금 시세 다운
df = quandl.get(dataset = 'WGC/GOLD_DAILY_USD',
start_date = '2000-01-01',
end_date = '2005-12-31')
df.reset_index(drop = False, inplace = True)
# prophet 사용을 위해 데이터프레임 형식 맞추기
df.rename(columns = {'Date' : 'ds', 'Value' : 'y'}, inplace = True)# train / test 분해
train_indices = df.ds.apply(lambda x: x.year).values < 2005
df_train = df.loc[train_indices].dropna()
df_test = df.loc[~train_indices].reset_index(drop=True)model_prophet = Prophet(seasonality_mode='additive')
# 임의로 월별 계절성 추가(아래 파라미터는 rule of thumb)
## period = 30.5 (한달 일 수)
## fourier_order : Seasonality 파악을 위한 강도로 강도가 높을수록 더 유연하게 예측하나 너무 높을 시
## overfitting의 문제가 생김
model_prophet.add_seasonality(name='monthly', period=30.5, fourier_order=5)
model_prophet.fit(df_train)# make_future_dataframe : 얻고자 하는 기간(일 단위)을 표시
df_future = model_prophet.make_future_dataframe(periods=365)
# 예측 생성
df_pred = model_prophet.predict(df_future)
model_prophet.plot(df_pred)
plt.tight_layout()
plt.show()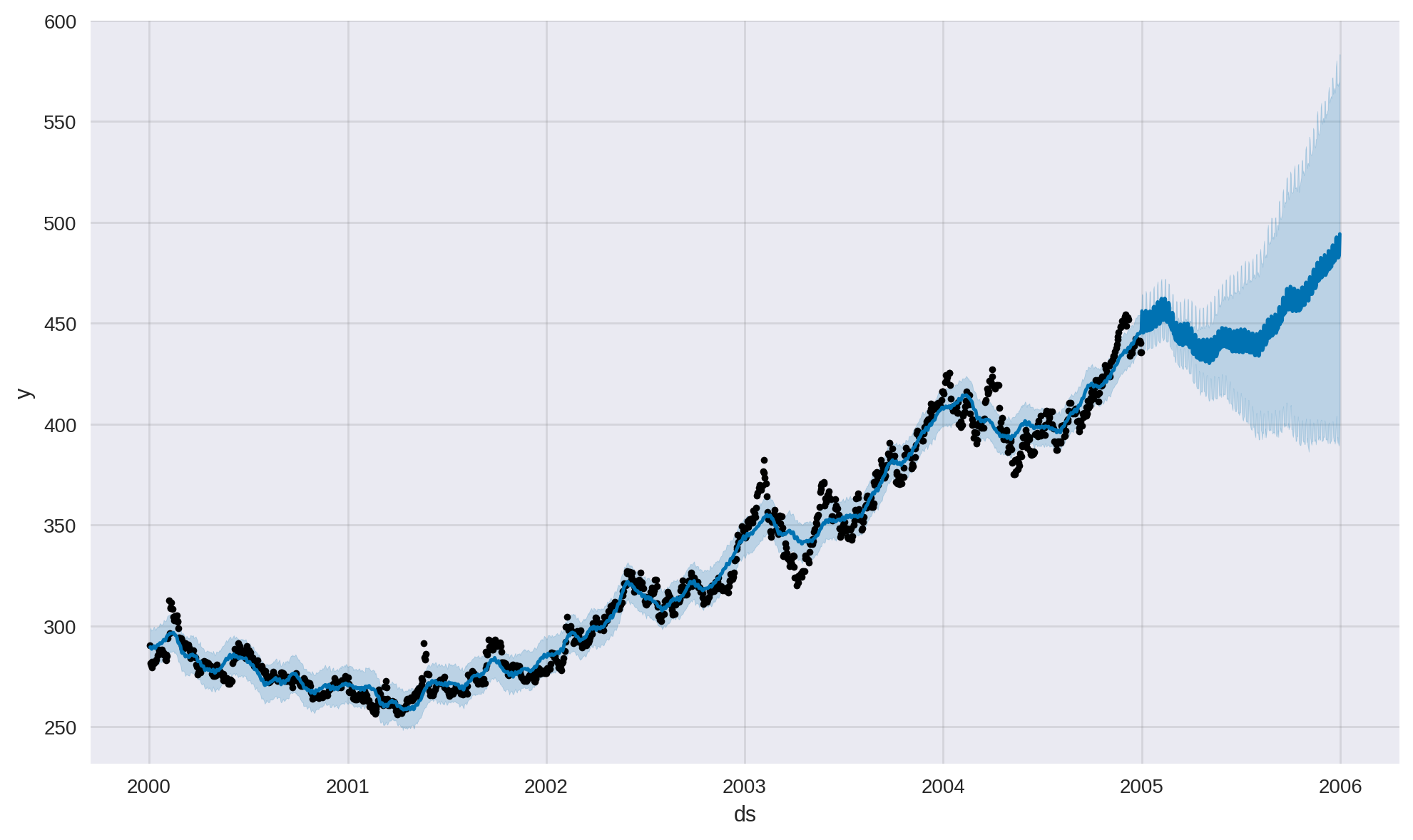
- 검은 점 = 실제 관측값
- 파란 선 = 적합화를 나타냄 / 모델이 데이터의 noise를 평활화해 제거했기 때문에 검은 점과 정확히 일치하지는 않음
- 파란색 간격 = 불확실성의 정량화 결과
- 2005 ~ 2006 = 예측값
# 시계열 분해
model_prophet.plot_components(df_pred)
- 전반적인 trend는 증가하고 있음
- yearly 단위로 보았을 때 금 가격이 연중 하락해, 연초와 연말에 더 높은 것으로 보임.
- monthly 단위에서도 변동은 있지만 yearly에 비해 그 변화 규모는 훨씬 작음.
- weekly 단위에는 변동은 거의 없음. 주말에는 시세가 없어 보이지 않음.
예측값과 실제 금 가격을 시각화하여 비교해 보자.
# test셋과 합쳐서 실제 값과 예측값 비교
selected_columns = ['ds', 'yhat_lower', 'yhat_upper', 'yhat']
df_pred = df_pred.loc[:, selected_columns].reset_index(drop=True)
# test 집합에 있던 날짜만 유지
df_test = df_test.merge(df_pred, on=['ds'], how='left')
df_test.ds = pd.to_datetime(df_test.ds)
df_test.set_index('ds', inplace=True)fig, ax = plt.subplots(1, 1)
ax = sns.lineplot(data=df_test[['y', 'yhat_lower',
'yhat_upper', 'yhat']])
ax.fill_between(df_test.index,
df_test.yhat_lower,
df_test.yhat_upper,
alpha=0.3)
ax.set(title='Gold Price - actual vs. predicted',
xlabel='Date',
ylabel='Gold Price ($)')
plt.tight_layout()
#plt.savefig('images/ch3_im5.png')
plt.show()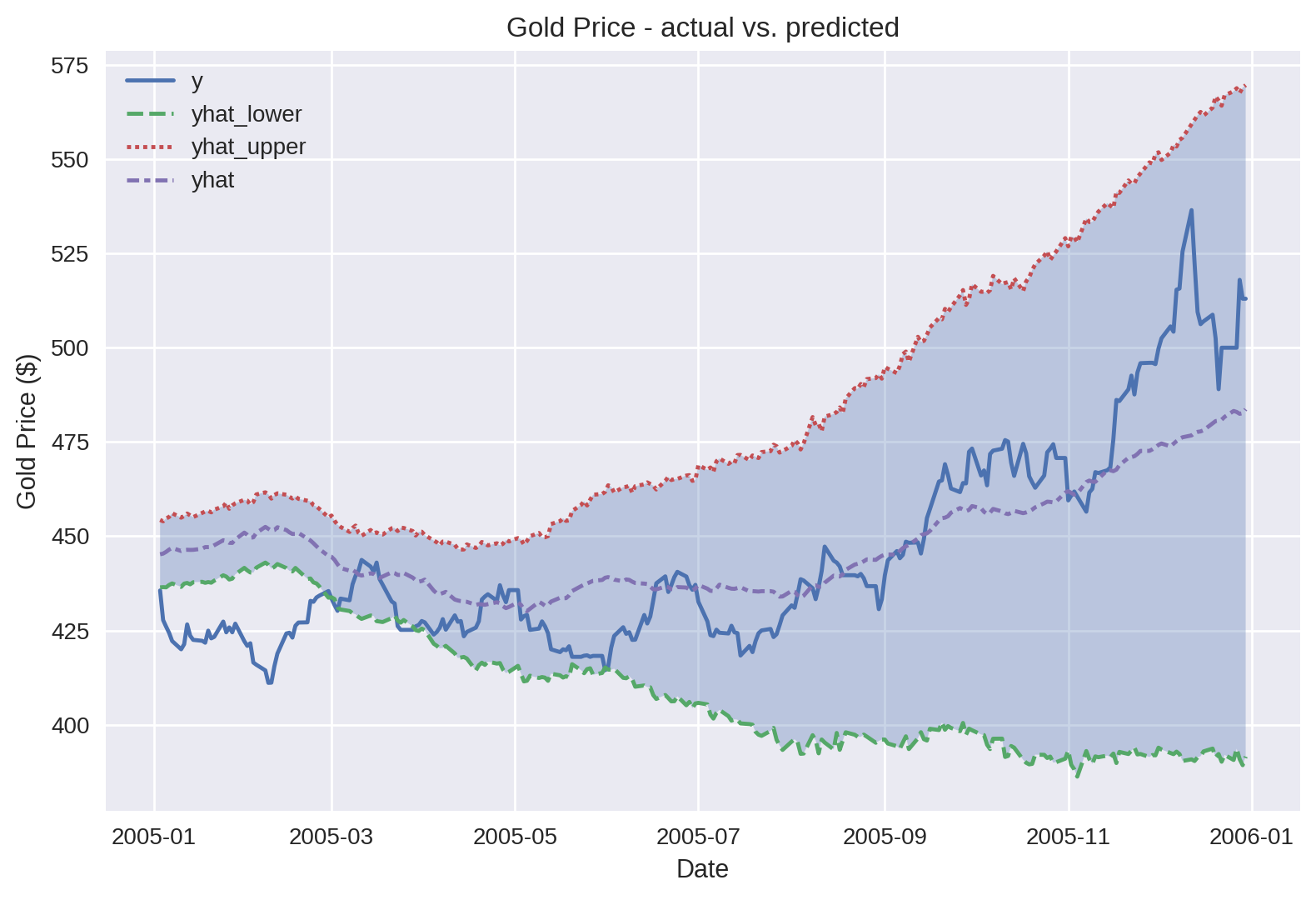
시각적으로 보았을 때 꽤 잘 예측한 것으로 보인다.
Prophet 튜토리얼은 아래 링크에서 잘 설명해두어 많이 참고하였다.
시계열 예측 패키지 Prophet 소개
Prophet을 이용하여 시계열 데이터를 예측하는 방법에 대해 소개합니다.
hyperconnect.github.io
(해당 게시물 학습을 위한 임의적 설정이므로, 수익을 대변하지 않습니다.)
Ref
- 금융 파이썬 쿡북, 에릭 르윈슨.
- HYPER CONNECT 기술 블로그, 시계열 예측 패키지 Prophet 소개
'Advance Deep Learning > [Quant] 금융 파이썬 쿡북' 카테고리의 다른 글
| 시계열 모델링 - ARIMA (0) | 2023.02.07 |
|---|---|
| 시계열 모델링 - 지수 평활법 (0) | 2023.02.03 |
| 시계열 정상성 검정 & 교정 (0) | 2023.02.02 |
| 볼린저 밴드 계산과 매수/매도 전략 테스트 (1) | 2023.01.30 |
| 단순이동평균(SMA)를 기반으로 전략 백테스팅 (0) | 2023.01.30 |