[Statistical Learning] KNN : K-nearest neighbors

 Qualtitative predict 문제에서는 사용되는  Bayes Classifier는 trainging data가 주어졌을 때 response data의 조건부 분포를 알고 있는 경우에만 가능했다. 하지만 실제 데이터는 그렇지 않은 경우가 대부분이다. 이때 사용되는 방법 중 하나가 KNN이다.

 

 training data가 주어졌을 때 response data의 조건부 분포를 모를 경우 이를 추정한 뒤에 training data가 속할 확률이 가장 큰 class를 예측해야 한다. 이런 방법론은 다양한데 그 중 하나가 KNN이다. 

 

 사전 설정된 양의 정수 K는 KNN classifier가 test observation인 X0와 가장 가깝다고 확인하는 traninig data의 point의 갯수이다. 이를 N0라 하면 class j에 속할 확률은 다음과 같이 표현할 수 있다. 

 위 수식으로 계산된 특정 클래스에 속할 확률 등 중 가장 큰 확률을 가진 class에 test observation X0를 배정하게 된다. 

 

 아래의 예시를 통해 보면 더욱 이해하기 쉽다. 검은색 크로스 모양의 지점의 class를 예측하는 경우이다.

 

K=3으로 설정한다면 KNN classifier는 크로스 지점과 가장 가가운 세개의 observation points를 찾는다. 이때 points들은 두 개의 파란색 클래스와 한 개의 주황색 클래스로 구성되어 있다. 파란색 클래스가 2/3 확률로 등장하기에 크로스 지점은 파란색 클래스라고 예측하게 된다.

좀 더 정확히 일반화하여 표현하면 ' test observations belongs to the most commonly-occuring class'이라고 할 수 있다.

 

 

 이렇게 분포를 추정해 분류한 KNN의 결과는 Bayes classfier와 비슷한 결과를 갖는다고 한다.

 

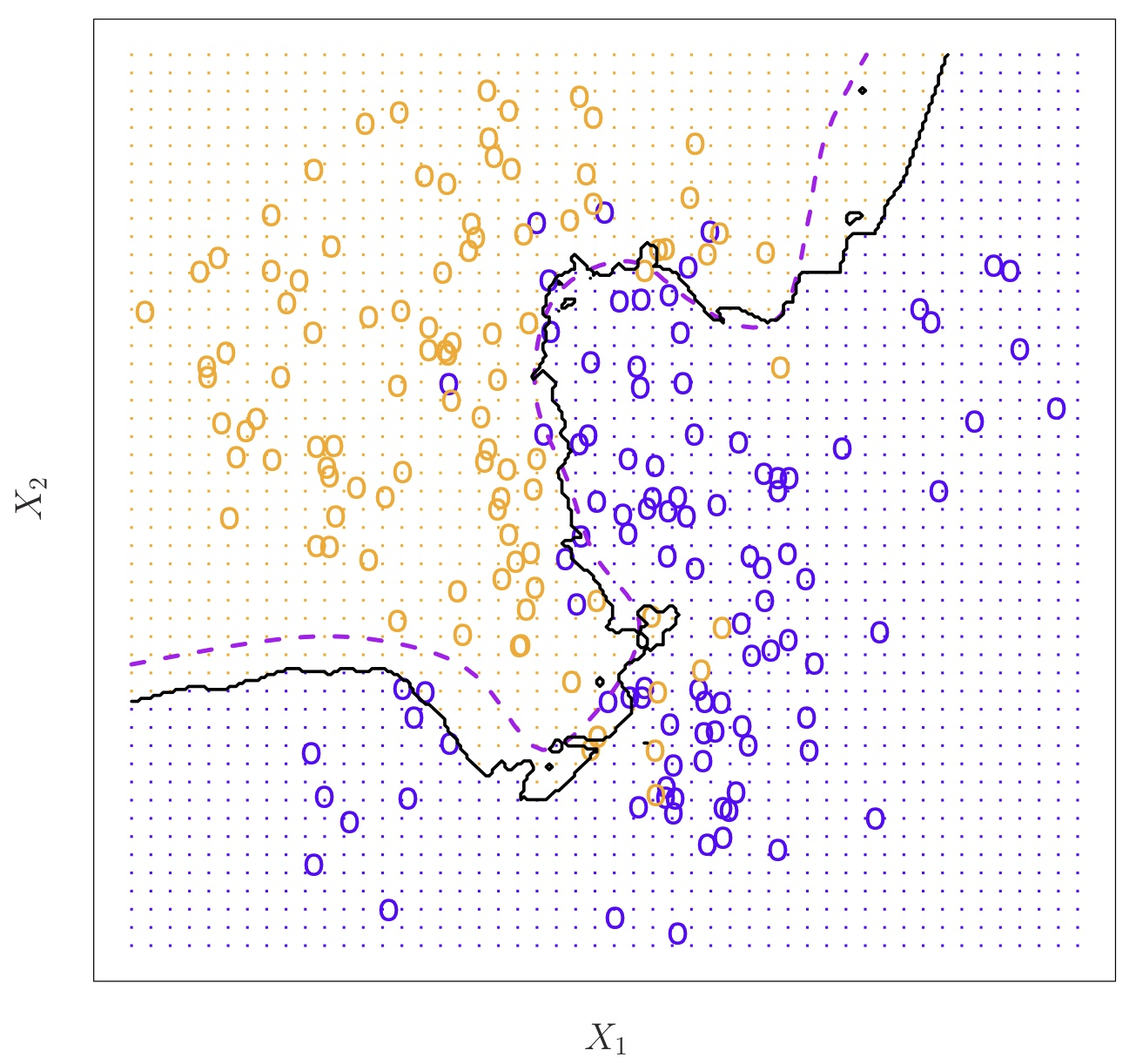
 다음과 같이 구성된 데이터를 K=10일 때 KNN을 사용해 분류했을 때 검은색 선을 기준으로 분류되고, Bayes classifier를 사용했을 때 보라색 선을 기준으로 분류된다. 분류된 결과가 상당히 유사함을 알 수 있다. 

 

 

이제는 K의 설정값에 따른 차이점을 알아보자.

왼쪽 사진은 K=1, 오른쪽 사진은 K=100일 떄의 분류 결과이다. 

 

 

 K=1일 떄 decision boundary가 더 flexible 한 것을 알 수 있다. 

다시 말해, K가 커질수록 분류는 덜 flexible 해지고 linear과 유사한 decision boundary를 그리게 된다. 이는 다르게 Low-variance but high-bias라고 표현할 수 있다. flexible한 분류일수록 training error는 감소하지만 test error은 커질 수 있다. 

아래 그림은 1/K에 따른 training과 test error이다.

 

 

 x축이 1/K 값인데, 그림에서 알 수 있듯 K가 작을수록 training error는 끝없이 작아지지만 test error는 계속해서 커짐을 알 수 있다. 

특히 test error를 보면 U자 모양의 그래프를 띄는데 이 때의 최저점을 갖는 K로 설정하는 것이 unknown data를 예측하는데 가장 좋은 성능을 낸다고 할 수 있다.  여기서 등장하는 bias-variance tradeoff는 overfitting과도 관련되어 선택하기 어려운 task이다. 다양한 test error 측정방식으로 test error를 측정하고 optimal level of flexibilty를 설정하는 것이 중요하다.

 

 

파이썬 코드 참고자료 : https://needjarvis.tistory.com/715

KNN(k최근접) 알고리즘 설명 및 구현하기

---

Reference

 

- An introduction to Statistical Learning 2nd edition, Gareth James, 2.2장